题目内容
8．
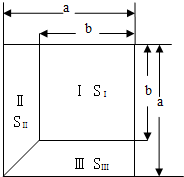根据图示，回答下列问题（1）大正方形的面积S是多少？
（2）梯形Ⅱ，Ⅲ的面积SⅡ，SⅢ，分别是多少？
（3）试求SⅡ+SⅢ与S-SⅠ的值．
（4）由 （3）你发现了什么？请用含a，b的式子表示你的结论．
分析 （1）由大正方形的边长求出面积S即可；
（2）利用梯形的面积公式表示出梯形Ⅱ，Ⅲ的面积SⅡ，SⅢ即可；
（3）分别求出SⅡ+SⅢ与S-SⅠ的值即可；
（4）根据（3）中的结论，得到SⅡ+SⅢ=S-SⅠ，表示即可．
解答 解：（1）大正方形的面积S=a2；
（2）根据题意得：SⅡ=$\frac{1}{2}$（a+b）（a-b）=$\frac{1}{2}$a2-$\frac{1}{2}$b2，SⅢ=$\frac{1}{2}$（a+b）（a-b）=$\frac{1}{2}$a2-$\frac{1}{2}$b2；
（3）根据题意得：SⅡ+SⅢ=a2-b2，S-SⅠ=a2-b2；
（4）根据（3）得：SⅡ+SⅢ=S-SⅠ=a2-b2．
点评 此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
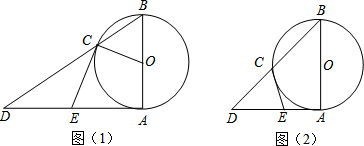
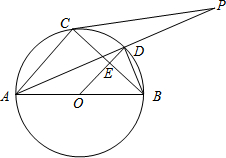如图，⊙O是以AB为直径的△ABC的外接圆，点D是劣弧$\widehat{BC}$的中点，连结AD并延长，与过C点的直线交于P，OD与BC相交于点E．
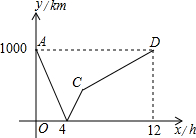如图所示，一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，设慢车行驶的时间为x小时，两车之间的距离为y千米，图中的折线表示y与x之间的函数关系，则快车的速度是$166\frac{2}{3}$千米/小时．
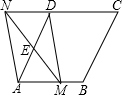如图，在菱形ABCD中，AB=4，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
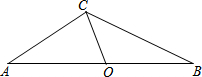如图，已知钝角三角形ABC，∠A=35°，OC为边AB上的中线，将△AOC绕着点O顺时针旋转，点C落在BC边上的点C′处，点A落在点A′处，联结BA′，如果点A、C、A′在同一直线上，那么∠BA′C′的度数为20°．