题目内容
2.点O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)?①如图1,若∠AOC=50°,求∠DOE的度数;
?②如图1,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(2)将图1中的∠COD按顺时针方向旋转至图2所示的位置.探究∠AOC与∠DOE的度数之间的关系,写出你的结论,并说明理由.

分析 (1)①首先求得∠COB的度数,然后根据角平分线的定义求得∠COE的度数,再根据∠DOE=∠COD-∠COE即可求解;
②解法与①相同,把①中的60°改成α即可;
(2)把∠AOC的度数作为已知量,求得∠BOC的度数,然后根据角的平分线的定义求得∠COE的度数,再根据∠DOE=∠COD-∠COE求得∠DOE,即可解决.
解答 解:(1)①∵∠AOC=50°
∴∠BOC=180°-∠AOC
=180°-50°
=130°
又∵OE平分∠BOC
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×130°=65°
又∵∠COD=90°
∴∠DOE=∠COD-∠COE
=90°-65°
=25°
②∠DOE=90°-$\frac{1}{2}$(180-α)
=90°-90°+$\frac{1}{2}$α=$\frac{1}{2}$α;
(2)∠DOE=$\frac{1}{2}$∠AOC,理由如下:
∵∠BOC=180°-∠AOC
又∵OE平分∠BOC
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-∠AOC)
=90°-$\frac{1}{2}$∠AOC
又∵∠DOE=90°-∠COE
=90°-(90°-$\frac{1}{2}$∠AOC)
=$\frac{1}{2}$∠AOC.
点评 本题考查了角度的计算,正确理解角平分线的定义,理解角度之间的和差关系是关键.

练习册系列答案
相关题目
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
13. 某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
并求得了A产品三次单价的平均数和方差:
$\overline{{x}_{A}}=5.9$;SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)补全“A、B产品单价变化的折线图”,B产品第三次的单价比上一次的单价降低了百分之多少?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件.
则A产品这四次单价的中位数是6.25元/件.
若A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,则B产品的第四次单价为3.75元/件.
 某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
$\overline{{x}_{A}}=5.9$;SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)补全“A、B产品单价变化的折线图”,B产品第三次的单价比上一次的单价降低了百分之多少?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件.
则A产品这四次单价的中位数是6.25元/件.
若A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,则B产品的第四次单价为3.75元/件.
 如图,四边形ABCD内接于⊙O,若⊙O的半径为6,∠A=130°,则扇形OBAD的面积为10π.
如图,四边形ABCD内接于⊙O,若⊙O的半径为6,∠A=130°,则扇形OBAD的面积为10π.
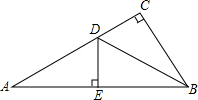 如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=3cm,则AC=9cm.
如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=3cm,则AC=9cm.