题目内容
11.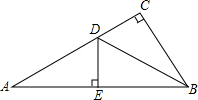 如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=3cm,则AC=9cm.
如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=3cm,则AC=9cm.
分析 先根据直角三角形的性质得出∠ABC的度数,再由线段垂直平分线的性质得出AD=BD,故可得出∠A=∠ABD=30°,故BD是∠ABC的角平分线,由此可得出DE的长,根据直角三角形的性质求出AD的长,进而可得出结论.
解答 解:∵在△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-30°=60°.
∵DE是线段AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD=30°,
∴BD是∠ABC的角平分线,
∴CD=DE=3cm,
∴AD=2DE=6cm,
∴AC=AD+CD=6+3=9cm.
故答案为:9.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
16.在半径为5cm的⊙O中,点P是⊙O内一点,且OP=3cm,则过点P的最短弦长是( )
| A. | 4cm | B. | 3cm | C. | 6cm | D. | 8cm |
3.下列命题中,①9的平方根是3;②9的平方根是±3;③-0.027没有立方根;④-3是27的负的立方根;⑤一个数的平方根等于它的算术平方根,则这个数是0;⑥$\sqrt{16}$的平方根是±4,其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列命题中,是真命题的是( )
| A. | 内错角相等 | B. | 如果$\frac{x-5}{2}=\frac{3-x}{3}$,那么x=4 | ||
| C. | 一个角的补角大于这个角 | D. | 同位角相等,两直线平行 |
 已知,线段AB=12,点O是AB的中点,C是线段AO上一点,且OC:OB=1:3,求线段AC的长.
已知,线段AB=12,点O是AB的中点,C是线段AO上一点,且OC:OB=1:3,求线段AC的长.
 小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息: