题目内容
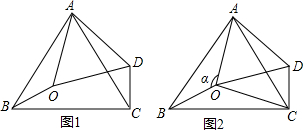
10. 如图,四边形ABCD内接于⊙O,若⊙O的半径为6,∠A=130°,则扇形OBAD的面积为10π.
如图,四边形ABCD内接于⊙O,若⊙O的半径为6,∠A=130°,则扇形OBAD的面积为10π.
分析 连结OB、OD,如图,先利用圆内接四边形的性质计算出∠C=180°-∠A=50°,再根据圆周角定理得到∠AOD=2∠C=100°,然后利用扇形的面积公式计算扇形OBAD的面积.
解答 解:连结OB、OD,如图,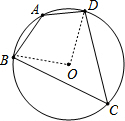 ∵∠A+∠C=180°,
∵∠A+∠C=180°,
∴∠C=180°-130°=50°,
∴∠AOD=2∠C=100°,
∴扇形OBAD的面积=$\frac{100•π•{6}^{2}}{360}$=10π.
故答案为10π.
点评 本题考查了扇形面积的计算:扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则 S扇形=$\frac{n}{360}$•πR2或S扇形=$\frac{1}{2}$lR(其中l为扇形的弧长).也考查了圆周角定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.以下列各组数为一个三角形的三边长,能构成直角三角形的是( )
| A. | 2,3,4 | B. | 3,4,5 | C. | 5,6,7 | D. | 7,8,9 |
20.下列命题中,是真命题的是( )
| A. | 内错角相等 | B. | 如果$\frac{x-5}{2}=\frac{3-x}{3}$,那么x=4 | ||
| C. | 一个角的补角大于这个角 | D. | 同位角相等,两直线平行 |
 已知,线段AB=12,点O是AB的中点,C是线段AO上一点,且OC:OB=1:3,求线段AC的长.
已知,线段AB=12,点O是AB的中点,C是线段AO上一点,且OC:OB=1:3,求线段AC的长.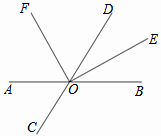 如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.