题目内容
11.关于x的一元二次方程ax2+bx+c=0(a≠0)给出下列说法:①若a+c=0,则方程必有两个实数根;②若a+b+c=0,则方程必有两个实数根;③若b=2a+3c,则方程有两个不等的实数根;④若b2-5ac<0,则方程一定没有实数根,其中说法正确的序号是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 利用c=-a可判断△=b2+4a2>0,从而根据判别式的意义可对①进行判断;利用c=-(a+b)得到△=b2-4ac=(2a+b)2≥0,则可根据判别式的意义对②进行判断;利用b=2a+3c得到△=4(a+c)2+5c2>0,则可根据判别式的意义对③进行判断;由于b2-5ac<0,不能判断△=b2-4ac=b2-5ac+ac与0的大小关系,则可根据判别式的意义对④进行判断.
解答 解:当a+c=0,即c=-a,则△=b2-4ac=b2+4a2>0,方程必有两个不相等的实数根,所以①正确;
当a+b+c=0,即c=-(a+b),则△=b2-4ac=b2+4a(a+b)=(2a+b)2≥0,方程必有两个实数根,所以②正确;
当b=2a+3c,则△=b2-4ac=(2a+3c)2-4ac=4(a+c)2+5c2>0,方程必有两个不相等的实数根,所以③正确;
当b2-5ac<0,△=b2-4ac=b2-5ac+ac可能大于0,所以不能判断方程根的情况,所以④错误.
故选A.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
2.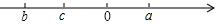 若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
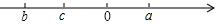 若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )| A. | a>b>c>0 | B. | c<b<0<a | C. | a>0>c>b | D. | c>b>0>a |
19.下列根式中,能与$\sqrt{2}$合并的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{30}$ |
6.下列图案中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列实数最小的是( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
3.化简$\frac{{m}^{2}}{m-3}$+$\frac{9}{3-m}$的结果是( )
| A. | m-3 | B. | m+3 | C. | $\frac{m+3}{m-3}$ | D. | $\frac{m-3}{m+3}$ |
20.在函数y=$\frac{\sqrt{3-x}}{x+2}$中,自变量x的取值范围是( )
| A. | x≤3且x≠-2 | B. | x≤3 | C. | x≠-2 | D. | x<3且x≠-2 |
 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )