题目内容
1. 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据等腰三角形三线合一的性质可得AD平分∠BAC,判断出②正确,根据角平分线上的点到角的两边的距离相等可得DE=DF,判断①正确;由全等三角形对应边相等可得AE=AF,判断出③正确;根据角平分线上的点到角的两边的距离相等判断出④正确.
解答 解:∵AB=AC,AD⊥BC,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF,故①正确;
在△ADE和△ADF中,
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴△ADE≌△ADF(HL),
∴∠ADE=∠ADF,
∴DA平分∠EDF,故②正确;
AE=AF,故③正确;
∵AD平分∠BAC,
∴AD上的点到AB、AC两边距离相等,故④正确;
综上所述,正确的有①②③④共4个.
故选:D.
点评 本题考查了等腰三角形的性质,角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,熟记各性质与全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
11.关于x的一元二次方程ax2+bx+c=0(a≠0)给出下列说法:①若a+c=0,则方程必有两个实数根;②若a+b+c=0,则方程必有两个实数根;③若b=2a+3c,则方程有两个不等的实数根;④若b2-5ac<0,则方程一定没有实数根,其中说法正确的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
12.若关于x的分式方程$\frac{ax}{x-2}$=$\frac{4}{x-2}$+1有解,则a的值为( )
| A. | a≠1 | B. | a≠2 | C. | a≠-1且a≠-2 | D. | a≠1且a≠2 |
9.已知三条不同的直线a,b,c在同一平面内,下列四个命题中假命题是( )
| A. | 如果a∥b,a⊥c,那么b⊥c | B. | 如果b∥a,c∥a,那么b∥c | ||
| C. | 如果b⊥a,c⊥a,那么b⊥c | D. | 如果b⊥a,c⊥a,那么b∥c |
6.如果a与3-1互为相反数,则a的值是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
13.2015年CCTV《谁是球王》争霸赛,武汉市第12初级中学梦想队披荆斩棘勇夺全国亚军,为武汉少年、湖北足球争光添彩!梦想队10名运动员的身高(单位:m)如下表所示:
那么这些运动员身高的中位数是( )
| 身高(m) | 1.65 | 1.67 | 1.68 | 1.70 | 1.74 | 1.76 |
| 人数 | 1 | 2 | 2 | 3 | 1 | 1 |
| A. | 1.70 | B. | 1.69 | C. | 1.68 | D. | 3 |
10.如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上.将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2016为止,则AP2016=( )
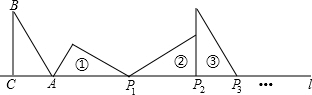

| A. | $2016+671\sqrt{3}$ | B. | $2015+672\sqrt{3}$ | C. | $2016+672\sqrt{3}$ | D. | $2015+671\sqrt{3}$ |
11.天气预报“明天永春县下雨的概率是40%”,是指( )
| A. | 明天该县有40%的时间会下雨 | B. | 明天该县有40%的区域会下雨 | ||
| C. | 明天该县下雨的可能性是40% | D. | 明天该县下雨的可能性很小 |
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,E是AB的中点,∠ACD=1.5∠DCE,则∠A=22.5°.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,E是AB的中点,∠ACD=1.5∠DCE,则∠A=22.5°.