题目内容
20.在函数y=$\frac{\sqrt{3-x}}{x+2}$中,自变量x的取值范围是( )| A. | x≤3且x≠-2 | B. | x≤3 | C. | x≠-2 | D. | x<3且x≠-2 |
分析 根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:由题意得,3-x≥0且x+2≠0,
解得x≤3且x≠-2.
故选A.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.关于x的一元二次方程ax2+bx+c=0(a≠0)给出下列说法:①若a+c=0,则方程必有两个实数根;②若a+b+c=0,则方程必有两个实数根;③若b=2a+3c,则方程有两个不等的实数根;④若b2-5ac<0,则方程一定没有实数根,其中说法正确的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
15.-2018的绝对值的倒数是( )
| A. | -$\frac{1}{2018}$ | B. | 2018 | C. | $\frac{1}{2018}$ | D. | -2018 |
5.下列五家银行行标中,既是中心对称图形,又是轴对称图形的个数有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
12.若关于x的分式方程$\frac{ax}{x-2}$=$\frac{4}{x-2}$+1有解,则a的值为( )
| A. | a≠1 | B. | a≠2 | C. | a≠-1且a≠-2 | D. | a≠1且a≠2 |
9.已知三条不同的直线a,b,c在同一平面内,下列四个命题中假命题是( )
| A. | 如果a∥b,a⊥c,那么b⊥c | B. | 如果b∥a,c∥a,那么b∥c | ||
| C. | 如果b⊥a,c⊥a,那么b⊥c | D. | 如果b⊥a,c⊥a,那么b∥c |
10.如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上.将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2016为止,则AP2016=( )
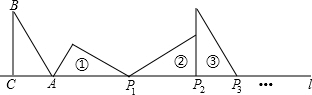

| A. | $2016+671\sqrt{3}$ | B. | $2015+672\sqrt{3}$ | C. | $2016+672\sqrt{3}$ | D. | $2015+671\sqrt{3}$ |
 如图,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.若反比例函数y=$\frac{m}{x}$(x>0)的图象与线段AC有公共点,则m的取值范围为1≤m≤4.
如图,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.若反比例函数y=$\frac{m}{x}$(x>0)的图象与线段AC有公共点,则m的取值范围为1≤m≤4.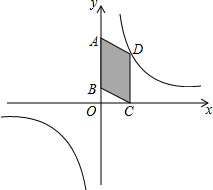 如图,平行四边形ABCD的一边AB在y轴上,顶点C在x轴上,顶点D在双曲线y=$\frac{6}{x}$上,则平行四边形ABCD的面积是( )
如图,平行四边形ABCD的一边AB在y轴上,顶点C在x轴上,顶点D在双曲线y=$\frac{6}{x}$上,则平行四边形ABCD的面积是( )