题目内容
在元旦联欢会上,有一个开盒有奖的游戏,两只外观一样的盒子,一只装有奖品,一只是空的,游戏规定:每人每次游戏时主持人先混合盒子再拿出来,参加游戏的同学随机打开其中一只,若有奖品,就获得该奖品,若是空盒子,就表演一个节目.
(1)两个人参加游戏,都获奖的概率为 .
(2)n个人参加游戏,全部获奖的概率为 .
(3)现取三只外观一样的盒子,一只内有奖品,另两只空盒子,游戏规则不变.两个人参加游戏,用画树形图法求至少有一个人表演节目的概率.
(1)两个人参加游戏,都获奖的概率为
(2)n个人参加游戏,全部获奖的概率为
(3)现取三只外观一样的盒子,一只内有奖品,另两只空盒子,游戏规则不变.两个人参加游戏,用画树形图法求至少有一个人表演节目的概率.
考点:列表法与树状图法
专题:计算题
分析:(1)每个人获奖的概率为
,然后利用概率的乘法计算两人都获奖的概率;
(2)与(1)的计算方法一样;
(3)利用树状图展示所有9种等可能的结果数,可以得到两个人都获得奖品的占1种,至少有一个人表演一个节目的结果数为8,于是可根据概率公式求出至少有一个人表演节目的概率.
| 1 |
| 2 |
(2)与(1)的计算方法一样;
(3)利用树状图展示所有9种等可能的结果数,可以得到两个人都获得奖品的占1种,至少有一个人表演一个节目的结果数为8,于是可根据概率公式求出至少有一个人表演节目的概率.
解答:解:(1)两个人参加游戏,都获奖的概率=
×
=
;
(2)n个人参加游戏,全部获奖的概率=
=
;
(3)画树状图为:

共有9种等可能的结果数,其中两个人都获得奖品的占1种,
所以至少有一个人表演节目的概率=
.
故答案为
,
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)n个人参加游戏,全部获奖的概率=
| ||||||||
n个
|
| 1 |
| 2n |
(3)画树状图为:

共有9种等可能的结果数,其中两个人都获得奖品的占1种,
所以至少有一个人表演节目的概率=
| 8 |
| 9 |
故答案为
| 1 |
| 4 |
| 1 |
| 2n |
点评:本题考查了列表法与画树状图法:利用列表法或画树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求解.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
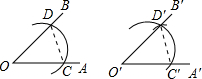 用直尺和圆规作一个角等于已知角的示意图如图,则说明∠D′O′C′=∠DOC的依据是( )
用直尺和圆规作一个角等于已知角的示意图如图,则说明∠D′O′C′=∠DOC的依据是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
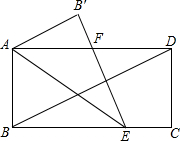 如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.
如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.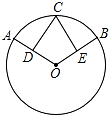 如图,D、E分别是半径OA和OB的中点,
如图,D、E分别是半径OA和OB的中点,
 如图,点P是△ABC中两外角∠DBC与∠ECB平分线的交点,试探索∠BPC和∠A的数量关系.
如图,点P是△ABC中两外角∠DBC与∠ECB平分线的交点,试探索∠BPC和∠A的数量关系.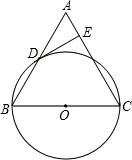 已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.