题目内容
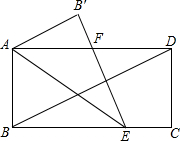 如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.
如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.(1)证明:∠B′AD=∠ADB;
(2)判断△AEF的形状,并说明;
(3)设AB=x,求△AEF的面积S与x的函数关系式.
考点:翻折变换(折叠问题)
专题:
分析:(1)证明AB′∥BD,即可解决问题.
(2)证明∠AEB=∠AEB′;证明∠FAE=∠BEA,得到∠AEB′=∠FAE,即可解决问题.
(3)证明△AB′F∽△DAB,得到
=
=2;由AB=AB′=x,得到B′F=
x;由勾股定理求出AF=
x,即可解决问题.
(2)证明∠AEB=∠AEB′;证明∠FAE=∠BEA,得到∠AEB′=∠FAE,即可解决问题.
(3)证明△AB′F∽△DAB,得到
| AB′ |
| B′F |
| AD |
| AB |
| 1 |
| 2 |
| ||
| 2 |
解答: 解:(1)如图,∵四边形ABCD为矩形,
解:(1)如图,∵四边形ABCD为矩形,
∴∠ABC=90°;
由题意得:B′E⊥BD,∠B′=∠B=90°,
∴AB′∥BD,
∴∠ADB=∠B′AD.
(2)△AEF是等腰三角形.
证明:根据题意可知:∠AEB=∠AEB′;
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAE=∠BEA,
∴∠AEB′=∠FAE,
∴△AEF是等腰三角形.
(3)∵∠B′=∠BAD,∠ADB=∠B′AD,
∴△AB′F∽△DAB,
∴
=
=2,而AB=AB′=x,
∴B′F=
x;
由勾股定理得:AF2=AB′2+B′F2,
∴AF=
x,
∴S=
=
x2.
 解:(1)如图,∵四边形ABCD为矩形,
解:(1)如图,∵四边形ABCD为矩形,∴∠ABC=90°;
由题意得:B′E⊥BD,∠B′=∠B=90°,
∴AB′∥BD,
∴∠ADB=∠B′AD.
(2)△AEF是等腰三角形.
证明:根据题意可知:∠AEB=∠AEB′;
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAE=∠BEA,
∴∠AEB′=∠FAE,
∴△AEF是等腰三角形.
(3)∵∠B′=∠BAD,∠ADB=∠B′AD,
∴△AB′F∽△DAB,
∴
| AB′ |
| B′F |
| AD |
| AB |
∴B′F=
| 1 |
| 2 |
由勾股定理得:AF2=AB′2+B′F2,
∴AF=
| ||
| 2 |
∴S=
| AF•AB |
| 2 |
| ||
| 4 |
点评:该题以矩形为载体,以翻折变换为方法,以考查矩形的性质、等腰三角形的判定、平行线的判定、三角形的面积公式等几何知识点为核心构造而成;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,求作一点P,使PA=PD,并且点P到∠BAC两边的距离相等(不写作法,但保留作图痕迹)
如图,求作一点P,使PA=PD,并且点P到∠BAC两边的距离相等(不写作法,但保留作图痕迹)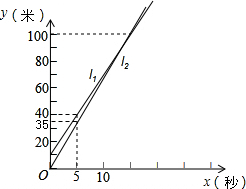 小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程y(米)分别与小明追赶时间x(秒)的函数关系如图所示.
小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程y(米)分别与小明追赶时间x(秒)的函数关系如图所示. 如图,已知AB=DC,AC=DB.求证:△ABC≌△DCB.
如图,已知AB=DC,AC=DB.求证:△ABC≌△DCB.