题目内容
5.(1)计算:$\frac{2}{x-1}$-$\frac{x-1}{{x}^{2}-2x+1}$(2)计算:(2$\sqrt{12}$-5$\sqrt{8}$)-($\sqrt{27}$-$\sqrt{18}$)
分析 (1)利用分式的通分、约分法则化简;
(2)根据二次根式的性质吧原式化简,合并同类二次根式即可.
解答 解:(1)$\frac{2}{x-1}$-$\frac{x-1}{{x}^{2}-2x+1}$
=$\frac{2(x-1)}{(x-1)^{2}}$-$\frac{x-1}{(x-1)^{2}}$
=$\frac{1}{x-1}$;
(2)计算:(2$\sqrt{12}$-5$\sqrt{8}$)-($\sqrt{27}$-$\sqrt{18}$)
=4$\sqrt{3}$-10$\sqrt{2}$-3$\sqrt{3}$+3$\sqrt{2}$
=$\sqrt{3}$-7$\sqrt{2}$.
点评 本题考查的是二次根式的加减法、分式的加减法,掌握分式的通分、约分法则、二次根式的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在Rt△ABC中,∠C=90°,tanA=$\frac{1}{2}$,BC=4,则AC的值为( )
| A. | 8 | B. | 2 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
16.已知x=2是方程2x-5=x+m的解,则m的值是( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
20.计算$\sqrt{32}$÷$\sqrt{2}$×$\sqrt{3}$的结果估计在( )
| A. | 5至6之间 | B. | 6至7之间 | C. | 7至8之间 | D. | 8至9之间 |
10.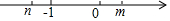 有理数m、n在数轴上的位置如图所示,下列判断正确的是( )
有理数m、n在数轴上的位置如图所示,下列判断正确的是( )
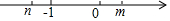 有理数m、n在数轴上的位置如图所示,下列判断正确的是( )
有理数m、n在数轴上的位置如图所示,下列判断正确的是( )| A. | m<0 | B. | m>1 | C. | n>-1 | D. | n<-1 |
14.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则$\frac{2017!}{2016!}$的值为( )
| A. | 2017 | B. | 2016 | C. | 2017! | D. | 2016! |
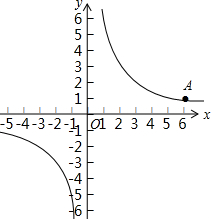 在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象过点A(6,1).
在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象过点A(6,1). 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=8cm,则AC=4cm.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=8cm,则AC=4cm.