题目内容
1.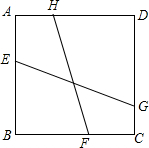 如图,正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长为1,FH的长为$\frac{\sqrt{5}}{2}$,求EG的长.
如图,正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长为1,FH的长为$\frac{\sqrt{5}}{2}$,求EG的长.
分析 可过点A作AM∥HF交BC于点M,过点A作AN∥EG交CD于点N,将△AND绕点A旋转到△APB,不难得出△APM和△ANM全等,那么可得出PM=MN,而MB的长可在Rt△ABM中根据AB和AM(即HF的长)求出.如果设DN=x,那么NM=PM=BM+x,MC=BC-BM=1-BM,因此可在直角三角形MNC中用勾股定理求出DN的长,进而可在Rt△AND中求出AN即EG的长.
解答 解:解:过点A作AM∥HF交BC于点M,过点A作AN∥EG交CD于点N,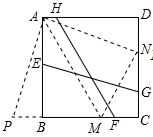
∵AB=1,AM=FH=$\frac{\sqrt{5}}{2}$,
在Rt△ABM中,BM=$\sqrt{A{M}^{2}-A{B}^{2}}$=$\frac{1}{2}$,将△AND绕点A旋转到△APB,
∴AP=AN.
∵EG与FH的夹角为45°,
∴∠MAN=45°,
∴∠DAN+∠MAB=45,即∠PAM=∠MAN=45°,
在△APM和△ANM中,有$\left\{\begin{array}{l}{AP=AN}\\{∠PAM=∠NAM}\\{AM=AM}\end{array}\right.$,
∴△APM≌△ANM(SAS),
∴PM=NM,
设DN=x,则NC=1-x,NM=PM=$\frac{1}{2}$+x,
在Rt△CMN中,($\frac{1}{2}$+x)2=$\frac{1}{4}$+(1-x)2,
解得x=$\frac{1}{3}$,
∴EG=AN=$\sqrt{1+{x}^{2}}$=$\frac{\sqrt{10}}{3}$,
答:EG的长为$\frac{\sqrt{10}}{3}$.
点评 本题主要考查了正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、图形的旋转变换等知识.通过辅助线或图形的旋转将所求的线段与已知的线段构建到一对全等或相似的三角形中是本题的基本思路.

| A. | 零除以任何数都等于零 | |
| B. | 1除以一个数就等于乘这个数的倒数 | |
| C. | 一个不等于零的有理数除以它的相反数等于-1 | |
| D. | 两数相除,商一定小于被除数 |
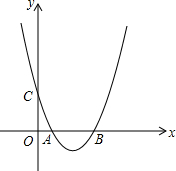 如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.