题目内容
12.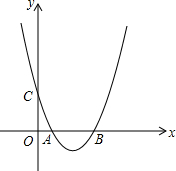 如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.(1)求点A、B、C的坐标;
(2)抛物线上有一点P(6m,5m),求S△BCP的值.
分析 (1)分别令x=0,y=0,解方程即可解决问题.
(2)把P(6m,5m),代入y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4,求出m的值,分两种情形计算即可.
解答 解:(1)令x=0则y=4,
∴点C(0,4),
令y=0则$\frac{1}{4}$x2-$\frac{5}{2}$x+4=0,解得x=2或8,
∴A(2,0),B(8,0),
(2)把P(6m,5m),代入y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4得5m=9m2-15m+4,
∴m=2或$\frac{2}{9}$,
∴P(12,10)或($\frac{12}{9}$,$\frac{10}{9}$),
①当P(12,10)时,S△PBC=S△PCO+S△PBO-S△BOC=$\frac{1}{2}$×4×12+$\frac{1}{2}$×8×10-$\frac{1}{2}$×4×8=48.
②当P′($\frac{12}{9}$,$\frac{10}{9}$)时,S△BCP′=S△BCO-S△COP′-S△OBP′=16-$\frac{1}{2}$×$4×\frac{12}{9}$-$\frac{1}{2}$×8×$\frac{10}{9}$=$\frac{80}{9}$,
∴△PBC的面积为48或$\frac{80}{9}$.
点评 本题考查抛物线与x轴的交点、三角形的面积等知识,解题的关键是灵活运用待定系数法,学会利用分割法求面积,属于中考常考题型.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
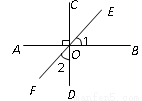
 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,求∠CEF的度数.
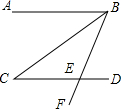
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,求∠CEF的度数. 如图,等边△ABC的边长为2,且DB=DC,∠BDC=120°,现有∠MDN=60°,其两边分别与AB,AC交于点M,N,连接MN,将∠MDN绕着D点旋转,使得M,N始终在边AB和边AC上.试判断在这一过程中,△AMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
如图,等边△ABC的边长为2,且DB=DC,∠BDC=120°,现有∠MDN=60°,其两边分别与AB,AC交于点M,N,连接MN,将∠MDN绕着D点旋转,使得M,N始终在边AB和边AC上.试判断在这一过程中,△AMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.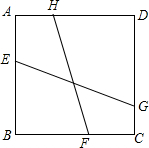 如图,正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长为1,FH的长为$\frac{\sqrt{5}}{2}$,求EG的长.
如图,正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长为1,FH的长为$\frac{\sqrt{5}}{2}$,求EG的长. ,求⊙O的直径.
,求⊙O的直径.