题目内容
5. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.
分析 由四边形ABCD为平行四边形,得到对边平行且相等,且对角线互相平分,根据两直线平行内错角相等得到两对角相等,进而确定出三角形MND与三角形CNB相似,由相似得比例,得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴MD:CB=DN:BN,
∵M为AD中点,
∴MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,即$\frac{MD}{CB}=\frac{1}{2}$,
∴$\frac{DN}{BN}=\frac{1}{2}$,即BN=2DN,
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6.
点评 此题考查了相似三角形的判定与性质,平行四边形的性质,熟练掌握相似三角形的判定与性质以及平行四边形的各种性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若函数y=$\frac{m-2}{x}$的图象在其所在的每一个象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
| A. | m<2 | B. | m<0 | C. | m>2 | D. | m>0 |
17. 如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )
如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )
 如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )
如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
14.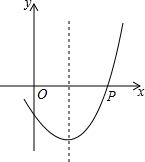 如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
 如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )
如图,抛物线y=ax2+bx+c的对称轴是直线x=1,且经过点P(3,0),则下列结论中正确的是( )| A. | abc<0 | B. | 2a+b<0 | C. | 3a+c<0 | D. | 4a-2b+c>0 |
 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=10,BC=16,则EF的长为3.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=10,BC=16,则EF的长为3.
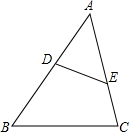 如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.
如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12. 一副三角板按如图方式摆放,且∠1比∠2大30°,则∠2的度数为30°.
一副三角板按如图方式摆放,且∠1比∠2大30°,则∠2的度数为30°.