题目内容
20.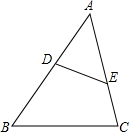 如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.
如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.
分析 由于∠B=∠AED,加上∠DAE=∠CAB,则可判断△ADE∽△ACB,根据相似三角形的性质得出对应边成比例,即可得出AB的长.
解答 解:∵∠B=∠AED,∠DAE=∠CAB,
∴△ADE∽△ACB,
∴$\frac{AE}{AB}=\frac{DE}{BC}$,即$\frac{6}{AB}=\frac{4}{8}$,
解得:AB=12.
故答案为:12.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用三角形相似的性质时,通过相似比计算相应边的长.

练习册系列答案
相关题目
15.一个扇形的弧长为5π,面积是15π,则该扇形的圆心角是( )
| A. | 120° | B. | 150° | C. | 210° | D. | 240° |
12.用棋子摆出下列一组图形:
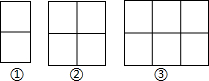
(1)填写表格:
(2)如果某一图形共有99枚棋子,你知道它是第几个图形吗?

(1)填写表格:
| 图形编号 | 1 | 2 | 3 | 4 | … | n |
| 图形中的棋子 | 6 | 9 | 12 | 15 | … | 3n+3 |
9.已知关于x的方程x2+mx-2=0的一个根是-1,则m的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 0或1 |
10.迎接学校“元旦”文艺汇演,八年级某班的全体同学捐款购买了表演道具,经过充分的排练准备,最终获得了一等奖.班长对全体同学的捐款情况绘制成下表:
由于填表时不小心把墨水滴在了统计表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的30%,结合上表回答下列问题:
(1)该班共有50名同学;
(2)该班同学捐款金额的众数是15元,中位数是12.5元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为
36度.
| 捐款金额 | 5元 | 10元 | 15元 | 20元 |
| 捐款人数 | 10人 | 15人 |  | 5人 |
(1)该班共有50名同学;
(2)该班同学捐款金额的众数是15元,中位数是12.5元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为
36度.
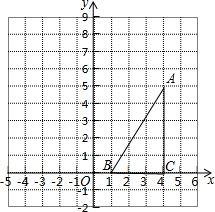 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度后,再沿y轴向上平移2个单位,根据所给的直角坐标系(O是坐标原点),解答下列问题:
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度后,再沿y轴向上平移2个单位,根据所给的直角坐标系(O是坐标原点),解答下列问题: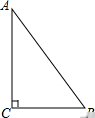 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.