题目内容
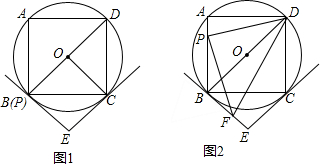
16.四边形ABCD是⊙O的内接正方形,AD=8,EB、EC是⊙O的两条,切点分别为B、C,P是边AB上的动点,连接DP.(1)如图1,当点P与点B重合时,连接OC.
①求∠E的度数;
②求CE的长度;
(2)如图2,当点P在AB上,且AP<$\frac{1}{2}$AB时,过点P作FP⊥DP于点P,交BE于点F,连接DF.
①试判断DP与FP之间的数量关系,并说明理由;
②若$\frac{BD}{DF}=\frac{10}{11}$,求DP的长度.
分析 (1)①根据切线的性质和正方形的性质,即可得到四边形OBEC的三个直角,随后即可求解;
②在等腰直角三角形BCE中运用勾股定理即可求出CE长度;
(2)①在AD上截取AM=AP,证明△DMP≌△PBF,即可得出结论;
②通过证明等腰直角三角形DPF∽等腰直角三角形ABD,即可求解.
解答 解:(1)如图1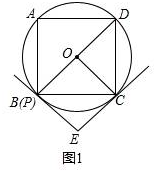
①∵EB、EC是⊙O的两条切线,
∴∠OCE=∠OBE=90°,
由四边形ABCD是⊙O的内接正方形,
可知,∠BOC=90°,
∴∠E=90°;
∵EB、EC是⊙O的两条切线,
∴EB=EC,
在直角三角形BEC中,
设EB=EC=x,由勾股定理得:x2+x2=82,
解得:x=$4\sqrt{2}$,
∴CE=$4\sqrt{2}$;
(2)如图2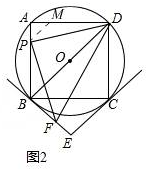
在AD上截取AM=AP,由∠A=90°可求∠AMP=∠APM=45°,
∴∠PMD=135°,
∵AD=AB,
∴MD=BP,
由(1)②知三角形BEC是等腰直角三角形,
∴∠CBE=45°,
∴∠PBF=135°,
∴∠PMD=∠PBF,
又可求:∠BPF+∠BFP=45°,
∵FP⊥DP,
∴∠MPD+∠BPD=45°,
∴∠MPD=∠BFP,
在△MPD和△BFP中,
$\left\{\begin{array}{l}{∠MPD=∠BFP}\\{∠PMD=∠PBF}\\{MD=BP}\end{array}\right.$,
∴△MPD≌△BFP,
DP=FP;
②由(2)①知,△DPF为等腰直角三角形,
又△DAB是等腰直角三角形,
∴△DPF∽△DAB,
∴$\frac{BD}{DF}=\frac{AD}{DP}$,
∵$\frac{BD}{DF}=\frac{10}{11}$,AD=8,
可求:DP=$\frac{44}{5}$.
点评 此题主要考查圆的综合问题,涉及到了正方形的相关性质,会运用切线性质和切线长定理,会构造全等与相似是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (2,1) | B. | (-2,-1) | ||
| C. | (2,-1) | D. | (1,2),(-1,2),(1,-2),(-1,-2) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | y=-2πx2+18πx | B. | y=2πx2-18πx | C. | y=-2πx2+36πx | D. | y=2πx2-36πx |
| A. | 57°42′ | B. | 57°82′ | C. | 147°42′ | D. | 147°82′ |
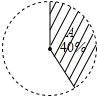 如图,扇形A的圆心角的度数为144°.
如图,扇形A的圆心角的度数为144°. 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连CM交BD于点N,ON=1,求BD的长.