题目内容
1.计算:(1)(m+1)(m-5)-m(m-6)
(2)(x-y+1)(x+y-1)-6x2y3÷3x2y2.
分析 (1)根据单项式乘多项式,多项式乘多项式的运算方法计算即可.
(2)根据完全平方公式,以及整式除法的运算方法计算即可.
解答 解:(1)(m+1)(m-5)-m(m-6)
=m2-5m+m-5-m2+6m
=2m-5
(2)(x-y+1)(x+y-1)-6x2y3÷3x2y2
=[x-(y-1)][x+(y-1)]-2y
=x2-(y-1)2-2y
=x2-y2+2y-1-2y
=x2-y2-1
点评 此题主要考查了整式的除法,以及完全平方公式的应用,解答此题的关键是熟练掌握整式的除法法则:(1)单项式除以单项式,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.(2)多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
12.在平面直角坐标系中,已知点P的坐标是(-1,-2),则点P关于原点对称的点的坐标是( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,2) | D. | (2,1) |
9. 如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )
如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )
 如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )
如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 5 |
16.小明解方程组x+y=■的解为x=5,由于不小心滴下了两滴墨水,刚好把$\left\{\begin{array}{l}{2x-y=7}\\{y=★}\end{array}\right.$两个数■和★遮住了,则这个数■和★的值为( )
| A. | $\left\{\begin{array}{l}{■=8}\\{★=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{■=8}\\{★=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{■=5}\\{★=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{■=3}\\{★=8}\end{array}\right.$ |
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )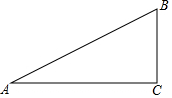 如图,Rt△ABC中,∠C=90°,∠A=30°.
如图,Rt△ABC中,∠C=90°,∠A=30°. 如图是由5个相同的小立方体搭成的一个几何体,从左面看这个几何体,看到的形状图是( )
如图是由5个相同的小立方体搭成的一个几何体,从左面看这个几何体,看到的形状图是( )


