题目内容
13．解方程：（1）4x2-9=0
（2）x（2x-5）=4x-10．
分析 （1）直接开平方法求解可得；
（2）因式分解法求解可得．
解答 解：（1）∵4x2=9，
∴x2=$\frac{9}{4}$，
则x=±$\frac{3}{2}$；
（2）∵x（2x-5）-2（2x-5）=0，
∴（2x-5）（x-2）=0，
则2x-5=0或x-2=0，
解得：x=$\frac{5}{2}$或x=2．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{-a+b}{-a-b}=\frac{a+b}{a-b}$ | |
| B． | $\frac{0.4a-0.09b}{0.8c+0.06d}=\frac{4a-9b}{8c+6d}$ | |
| C． | $\frac{{{b^2}-{a^2}}}{a+b}=a-b$ | |
| D． | $\frac{{1-\frac{1}{3}a}}{{a+\frac{1}{5}}}=\frac{15-5a}{15a+3}$ |
8．将二次函数y=x2的图象向左平移1个单位，则平移后的二次函数的解析式为（ ）
| A． | y=x2-1 | B． | y=x2+1 | C． | y=（x-1）2 | D． | y=（x+1）2 |
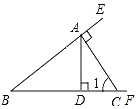如图，已知点A是射线BE上一点，过A作CA⊥BE交射线BF于点C，AD⊥BF交射线BF于点D，给出下列结论：