题目内容
9. 如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )
如图,长方形纸片ABCD的边AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则图中△EFC的面积为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 5 |
分析 根据翻折变换的性质可得∠AEF=∠CEF,再根据两直线平行,内错角相等可得∠AEF=∠CFE,然后求出∠CEF=∠CFE,证出CE=CF,根据翻折的性质可得AE=CE=CF,设CE=x,表示出BE,然后利用勾股定理列方程求出CF,根据三角形的面积公式列式计算即可得解.
解答 解:由翻折的性质得,∠AEF=∠CEF,
∵矩形对边AB∥CD,
∴∠AEF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF;
∵长方形纸片沿EF折叠点A与点C重合,
∴AE=CE=CF,
设AE=CE=CF=x,则BE=4-x,
∵四边形ABCD是矩形,
∴BC=AD=2,
在Rt△BCE中,BC2+BE2=CE2,
即22+(4-x)2=x2,
解得x=2.5,
∴CF=2.5,
∴△EFC的面积=$\frac{1}{2}$×2.5×2=2.5;
故选:C.
点评 本题考查了翻折变换的性质,平行线的性质,勾股定理,三角形的面积,熟记各性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
20.在△ABD与△ACD中,∠BAD=∠CAD,且B点,C点在AD边两侧,则不一定能使△ABD和△ACD全等的条件是( )
| A. | BD=CD | B. | ∠B=∠C | C. | AB=AC | D. | ∠BDA=∠CDA |
17. 如图,下列各数中,数轴上点A表示的数可能是( )
如图,下列各数中,数轴上点A表示的数可能是( )
 如图,下列各数中,数轴上点A表示的数可能是( )
如图,下列各数中,数轴上点A表示的数可能是( )| A. | 4的算术平方根 | B. | 4的立方根 | C. | 4的平方根 | D. | 8的算术平方根 |
4.下列各式从左到右的变形正确的是( )
| A. | $\frac{-a+b}{-a-b}=\frac{a+b}{a-b}$ | |
| B. | $\frac{0.4a-0.09b}{0.8c+0.06d}=\frac{4a-9b}{8c+6d}$ | |
| C. | $\frac{{{b^2}-{a^2}}}{a+b}=a-b$ | |
| D. | $\frac{{1-\frac{1}{3}a}}{{a+\frac{1}{5}}}=\frac{15-5a}{15a+3}$ |
14.传统佳节“春节”临近,剪纸民俗魅力四射,对称现象无处不在.观察下面的四幅剪纸,其中是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
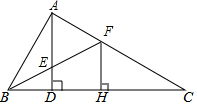 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线BF交AD于点E,交AC于点F,FH⊥BC于点H,求证:AE=FH.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线BF交AD于点E,交AC于点F,FH⊥BC于点H,求证:AE=FH. 已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.
已知:如图,AB⊥AC,且AB=AC,AD=AE,BD=CE.求证:AD⊥AE.