题目内容
2. 如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )
如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )| A. | $\frac{3-\sqrt{5}}{3}$ | B. | $\frac{3-\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{3}$ |
分析 设S△COD的面积为S1,S△AOB的面积为S2,由题中条件建立关于S1•S2的方程,解方程得出S1•S2之间的关系,进而可求解a、b之间的关系.
解答 解:设S△COD的面积为S1,S△AOB的面积为S2,由SABCD=S,
∵AB∥CD,
∴S△ABD=S△ABC,
∴S△ABD-S△AOB=S△ABC-S△AOB,
∴S△AOD=S△BOC=$\frac{1}{5}$S,得S1+S2=S-2×$\frac{1}{5}$S=$\frac{3}{5}$S,①
∵$\frac{{S}_{1}}{{S}_{△BOC}}$=$\frac{OD}{OB}$=$\frac{{S}_{△AOD}}{{S}_{2}}$,
∴S1•S2=S△BOC•S△AOD=$\frac{1}{25}$S2,②
联立①、②$\left\{\begin{array}{l}{{S}_{1}{+S}_{2}=\frac{3}{5}S}\\{{S}_{1}{•S}_{2}=\frac{1}{25}{S}^{2}}\end{array}\right.$,
∵△COD∽△AOB,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{{a}^{2}}{{b}^{2}}$,③
∵a<b,∴S1<S2,解方程组得S1=$\frac{3-\sqrt{5}}{5}$S,S2=$\frac{3+\sqrt{5}}{5}$S,
代入③得$\frac{a}{b}$=$\frac{3-\sqrt{5}}{2}$,
故选B.
点评 本题主要考查了梯形的性质以及相似三角形的判定及性质以及面积的问题,能够通过方程的思想建立等式是解答此题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | 2(2a-b)=4a-2b | C. | (a2)3=a5 | D. | a6÷a2=a3 |
2.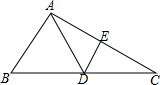 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )| A. | 13 | B. | 15 | C. | 17 | D. | 19 |
7.在数$\frac{22}{7}$,0,$\frac{π}{2}$,-1.414中,有理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11. 甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )
甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )
①乙在1.4小时后改变速度;
②甲乙两次相遇间隔为2小时;
③行驶完全程,乙比甲多用了2.4小时;
④两人的平均速度差为3.75千米/时.
 甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )
甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )①乙在1.4小时后改变速度;
②甲乙两次相遇间隔为2小时;
③行驶完全程,乙比甲多用了2.4小时;
④两人的平均速度差为3.75千米/时.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.数据-1,2,3,0,1的平均数( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
