题目内容
2.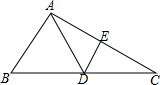 如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )| A. | 13 | B. | 15 | C. | 17 | D. | 19 |
分析 根据线段垂直平分线性质得出AD=DC,AE=CE=4,求出AC=8,AB+BC=15,求出△ABD的周长为AB+BC,代入求出即可.
解答 解:∵AC的垂直平分线分别交AC、BC于E,D两点,
∴AD=DC,AE=CE=4,
即AC=8,
∵△ABC的周长为23,
∴AB+BC+AC=23,
∴AB+BC=23-8=15,
∴△ABD的周长为AB+BD+AD=AB+BD+CD=AB+BC=15,
故选B.
点评 本题考查了线段垂直平分线性质的应用,能熟记线段垂直平分线性质定理的内容是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
17.下列各数中,最小的数是( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | -3 | D. | -2 |
2. 如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )
如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )
 如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )
如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )| A. | $\frac{3-\sqrt{5}}{3}$ | B. | $\frac{3-\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{3}$ |
19.若$\sqrt{\frac{{x}^{2}}{4{y}^{2}}}$=-$\frac{x}{2y}$成立,则x、y符合的条件是( )
| A. | x≤0,y≠0 | B. | x≤0,y为一切实数 | C. | x<0,y≠0 | D. | 以上都不对 |
20. 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
(1)试说明a=2时,四边形OMAB是菱形.
(2)当a的值分别取1,2,3时,分别计算s的值,将其填入如表
(3)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,当四边形OMAB为正方形时,a=2,m=$\frac{1}{2}$.
(4)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,s=4m3(用含m的代数式表示)
 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.(1)试说明a=2时,四边形OMAB是菱形.
(2)当a的值分别取1,2,3时,分别计算s的值,将其填入如表
| a | 1 | 2 | 3 |
| s |
(4)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,s=4m3(用含m的代数式表示)

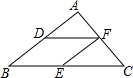 在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )
在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( ) 如图,AB是⊙O的直径,点C,D都在⊙O上,∠ABC=50°,则∠BDC的大小是40°.
如图,AB是⊙O的直径,点C,D都在⊙O上,∠ABC=50°,则∠BDC的大小是40°.