题目内容
5.若关于x的函数y=mx2-2x+1图象与x轴仅有一个公共点,则m值为0或1.分析 若m=0,一次函数与x轴只有一个交点,满足题意;若m不为0,根据抛物线图象与x轴只有一个交点,得到根的判别式等于0,即可求出m的值.
解答 解:若m=0,一次函数y=-2x+1与x轴只有一个交点,满足题意;
若m≠0,由二次函数y=mx2-2x+1图象与x轴只有一个交点,得到△=4-4m=0,
解得:m=1,
则m=0或1.
故答案为:0或1.
点评 此题考查了抛物线与x轴的交点,注意考虑两种情况进行分类讨论是正确解答的关键.

练习册系列答案
相关题目
19.已知反比例函数y=$\frac{4}{x}$,则当-4<x<-1时,y的取值范围是( )
| A. | 1<y<4 | B. | -4<y<-2 | C. | -4<y<-1 | D. | 2<y<4 |
15.某n边形共有n条对角线,那么n等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
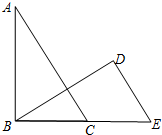 已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.
已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.
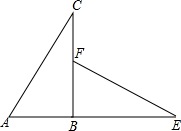 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答: