题目内容
4.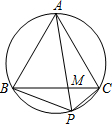 如图,点P为等边△ABC外接圆,劣弧为BC上的一点.
如图,点P为等边△ABC外接圆,劣弧为BC上的一点.(1)求∠BPC的度数;
(2)求证:PA=PB+PC.
分析 (1)根据圆内接四边形对角互补,可得答案;
(2)根据等边三角形的判定,可得△PCD的形状,根据全等三角形的判定与性质,可得BD与AP的关系,根据等量代换,可得答案.
解答 (1)解:∵四边形ABPC内接于圆,
∴∠BAC+∠BPC=180.
∵等边三角形ABC中,∠BAC=60°,
∴∠BPC=120°;
(2)证明:延长BP到D,使得DP=PC,连接CD.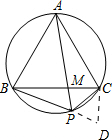
∵∠BPC=120,
∴∠CPD=60.
又∵PC=PD,
∴△PCD是等边三角形,
∴PC=CD,∠PCD=60°,
∴∠ACM+∠MCP=PCD+∠MCP,
即∠ACP=∠BCD.
∵等边三角形ABC中,
∴BC=AC.
∵$\widehat{PC}$所对的圆周角是∠DBC与∠PAC,
∴∠DBC=∠PAC.
在△DBC和△PAC中,
$\left\{\begin{array}{l}{∠DBC=∠PAC}\\{BC=AC}\\{∠BCD=∠ACP}\end{array}\right.$,
∴△DBC≌△PAC(ASA),
∴AP=BD.
∵BD=BP+DP,
∴AP=BP+DP,
∵DP=PC,
∴PA=PB+PC.
点评 本题考查了全等三角形的判定与性质,利用了圆内接四边形的性质,全等三角形的判定与性质,利用等式的性质得出∠ACM+∠MCP=PCD+∠MCP是解题关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.
如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.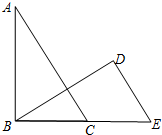 已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.
已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.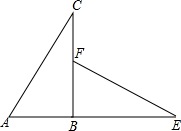 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答: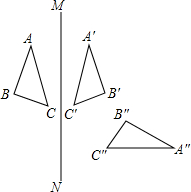 如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.