题目内容
在△ABC中,CB=CA,∠BCA=90°,D为BA任意一点,求证:BD2+AD2=2CD2.
考点:勾股定理,等腰直角三角形
专题:证明题
分析:作出图形,过点D作DE⊥BC于E,作DF⊥AC于F,判断出△BDE和△ADF都是等腰直角三角形,根据等腰直角三角形的性质可得DE=
BD,DF=
AD,再判断出四边形DECF是矩形,根据矩形的对边相等可得DE=CF,然后利用勾股定理列式整理即可得证.
| ||
| 2 |
| ||
| 2 |
解答: 证明:如图,过点D作DE⊥BC于E,作DF⊥AC于F,
证明:如图,过点D作DE⊥BC于E,作DF⊥AC于F,
∵CB=CA,∠BCA=90°,
∴∠A=∠B=45°,
∴△BDE和△ADF都是等腰直角三角形,
∴DE=
BD,DF=
AD,
又∵∠BCA=90°,
∴四边形DECF是矩形,
∴DE=CF,
在Rt△CDF中,DF2+CF2=CD2,
∴(
AD)2+(
BD)2=CD2,
∴BD2+AD2=2CD2.
 证明:如图,过点D作DE⊥BC于E,作DF⊥AC于F,
证明:如图,过点D作DE⊥BC于E,作DF⊥AC于F,∵CB=CA,∠BCA=90°,
∴∠A=∠B=45°,
∴△BDE和△ADF都是等腰直角三角形,
∴DE=
| ||
| 2 |
| ||
| 2 |
又∵∠BCA=90°,
∴四边形DECF是矩形,
∴DE=CF,
在Rt△CDF中,DF2+CF2=CD2,
∴(
| ||
| 2 |
| ||
| 2 |
∴BD2+AD2=2CD2.
点评:本题考查了勾股定理,等腰直角三角形的判定与性质,矩形的判定与性质,熟记各性质并作辅助线构造出等腰直角三角形和矩形是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛,则恰好选中甲、乙两位同学打第一场比赛的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在△ABC中,AD是BC边上的高,tanC=
如图,在△ABC中,AD是BC边上的高,tanC=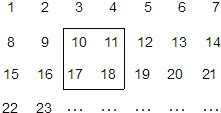 把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.
把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.