题目内容
11.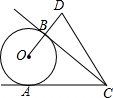 如图,CA、CB分别切⊙O于点A、B,延长0B到点D,使BD=OB,∠DCA=60°,求∠D的度数.
如图,CA、CB分别切⊙O于点A、B,延长0B到点D,使BD=OB,∠DCA=60°,求∠D的度数.
分析 连接OC,根据切线的性质定理求出∠OBC=∠DBC=90°,根据切线长定理求出∠ACO=∠BCO,根据线段垂直平分线性质求出DC=OC,根据等腰三角形的性质求出∠DCB=∠BCO,求出∠DCB,即可求出答案.
解答 解:如图,连接OC,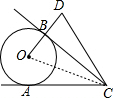
∵CA、CB分别切⊙O于点A、B,
∴∠BCO=∠ACO,∠OBC=90°,
∴BC⊥OD,
∵BD=OB,
∴OC=CD,
∴∠DCB=∠BCO,
∴∠DCB=$\frac{1}{3}$∠DCA,
∵∠DCA=60°,
∴∠DCB=20°,
∵∠DBC=∠OBC=90°,
∴∠D=90°-20°=70°.
点评 本题考查了切线的性质定理,切线长定理,线段垂直平分线性质,等腰三角形的性质的应用,能求出∠DCB的度数是解此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.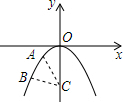 如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )
如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )
 如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )
如图,已知抛物线y=-x2上有A,B两点,其横坐标分别为-1,-2;在y轴上有一动点C,则AC+BC的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 5 |
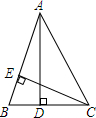 如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.
如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.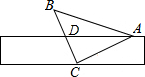 如图,将一个有45°角的三角板的直角顶点C在一张宽为1cm的纸带边沿上,另一个顶点A放在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则tan∠DAB=2-$\sqrt{3}$.
如图,将一个有45°角的三角板的直角顶点C在一张宽为1cm的纸带边沿上,另一个顶点A放在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则tan∠DAB=2-$\sqrt{3}$.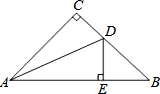 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DBE的周长8.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DBE的周长8.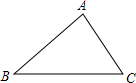 已知如图,AC=5,AB=7,CB=8,求∠C的度数.
已知如图,AC=5,AB=7,CB=8,求∠C的度数.