Question

10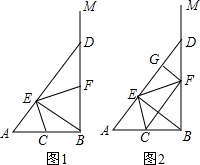．如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合），连结AD，作BE⊥AD，垂足为E，连结CE，过点E作EF⊥CE，交BD于F．
（1）求证：BF=FD；
（2）若∠A=45°，试判断四边形ACFE的形状，并说明理由；
（3）当∠A在什么范围取值时，线段DE上存在点G，满足条件DG=$\frac{1}{4}$DA．

Answer 1

分析 （1）根据直角三角形斜边上的中线等于斜边的一半，得到CE=BC．从而得到∠CBE=∠CEB，再根据等角的余角相等证明∠FBE=∠FEB，得到BF=EF．根据等角的余角相等以及等角对等边再进一步证明EF=DF，最后得到BF=DF．
（2）根据中位线定理得到AE∥CF由∠A=45°推出EF∥AC，从而得到结论．
（3）从若要满足的结论出发，结合上述结论进行分析，先探求∠D的取值范围，再进一步得到∠A的取值范围．

解答 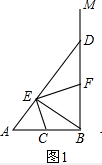（1）证明：如图1，在Rt△AEB中，
∵AC=BC，
∴CE=$\frac{1}{2}$AB，
∴CB=CE，
∴∠CEB=∠CBE．
∵∠CEF=∠CBF=90°，
∴∠BEF=∠EBF，
∴EF=BF．
∵∠BEF+∠FED=90°，∠EBD+∠EDB=90°，
∴∠FED=∠EDF．
∴BF=FD．
（2）解：由（1）BF=FD，而BC=CA，
∴CF∥AD，即AE∥CF．
∵∠A=45°，∠AEB=90，
∴∠ABE=90°-∠A=45°=∠A，
∴EA=EB，
∵AC=CB，
∴EC⊥AB，
∵EF⊥EC，
∴EF∥AB，
∵AE∥CF，
∴四边形ACFE是平行四边形．
（3）解：如图2，作GH⊥BD，垂足为H，则GH∥AB．
∵DG=$\frac{1}{4}$DA，
∴DH=$\frac{1}{4}$DB．
又F为BD中点，
∴H为DF的中点．
∴GH为DF的中垂线．
∴∠GDF=∠GFD．
∵点G在ED上，
∴∠EFD≥∠GFD．
∵∠EFD+∠FDE+∠DEF=180°，
∴∠GFD+∠FDE+∠DEF≤180度．
∴3∠EDF≤180度．
∴∠EDF≤60度．
又∠A+∠EDF=90°，
∴30°≤∠A＜90°．
∴当30°≤∠A＜90°时，
DE上存在点G，满足条件DG=$\frac{1}{4}$DA．

点评 本题考查了直角三角形斜边上的中线的性质，三角形的中位线性质、平行四边形判定等知识，熟练运用这些性质是解题的关键，第三问比较难不容易找到不等关系．