题目内容
15．（1）已知a、b、c均为实数，且$\sqrt{a-2}$+|b+1|+（c+3）2=0，求方程ax2+bx+c=0的根．（2）先化简，再求值：（$\frac{{a}^{2}-4}{{a}^{2}-4a+4}$-$\frac{1}{2-a}$）÷$\frac{2}{{a}^{2}-2a}$，其中a是方程x2+3x+1=0的根．
分析 （1）先根据非负数的性质求出a、b、c的值，再代入方程进行计算即可；
（2）先根据分式混合运算的法则把原式进行化简，再求出a2+3a的值代入进行计算即可．
解答 解：（1）
（2）原式=[$\frac{a+2}{a-2}$+$\frac{1}{a-2}$]•$\frac{a（a-2）}{2}$
=$\frac{a+3}{a-2}$•$\frac{a（a-2）}{2}$
=$\frac{{a}^{2}+3a}{2}$，
∵a是方程x2+3x+1=0的根，
∴a2+3a=-1，
∴原式=-$\frac{1}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
5．△ABC与△DEF相似，且相似比是$\frac{2}{3}$，则△DEF与△ABC的相似比是（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{4}{9}$ |
如图所示，∠C=∠D=90°，可使用“HL”判定Rt△ABC与Rt△ABD全等，则应添加一个条件是AC=AD．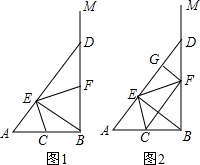
如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合），连结AD，作BE⊥AD，垂足为E，连结CE，过点E作EF⊥CE，交BD于F．
20．
如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C，若PC=2$\sqrt{5}$，⊙O的半径为（ ）
如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C，若PC=2$\sqrt{5}$，⊙O的半径为（ ）| A． | $\sqrt{5}$ | B． | $\frac{5}{2}$ | C． | 2$\sqrt{5}$ | D． | 3 |
一副三角板，如图所示叠放在一起，则图中∠α的度数是75°．
如图：在△ABC中，AD⊥BC，垂足是D．