题目内容
15. 在△ABC中,AB=8,BC=10,AC=6,动点P从点C出发,沿着CB运动,速度为每秒2个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
在△ABC中,AB=8,BC=10,AC=6,动点P从点C出发,沿着CB运动,速度为每秒2个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
分析 (1)过点A作AD⊥BC于点D,根据三角形的面积公式解答即可;
(2)根据等腰三角形的性质分三种情况进行解答即可.
解答 解:(1)过点A作AD⊥BC于点D,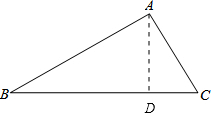
∵AB2+AC2=100 BC2=100
∴AB2+AC2=BC2
∴∠BAC=90° 即△ABC为直角三角形,
∴$\frac{AB×AC}{2}={S}_{△ABC}=\frac{BC×AD}{2}$
∴AD=4.8;
(2)当AC=PC时,
∵AC=6,
∴AC=PC=6,
∴t=3秒;
当AP=AC时,过点A作AD⊥BC于点D,
PD=DC
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=3.6,
∴PC=7.2,
∴t=3.6秒;
当AP=PC时,
∠PAC=∠C
∵∠BAC=90°
∴∠BAP+∠PAC=90°
∠B+∠C=90°
∴∠BAP=∠B
∴PB=PA
∴PB=PC=5
∴t=2.5
综上所述,t=3秒或3.6秒或2.5秒.
点评 此题考查等腰三角形的判定和性质,关键是根据等腰三角形的性质分三种情况进行解答.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
10.等腰三角形一边长为2,周长为5,则它的腰长为( )
| A. | 2 | B. | 5 | C. | 1.5 | D. | 1.5或2 |
20.由二次函数y=2(x-3)2+1可知( )
| A. | 其图象的开口向下 | B. | 其图象的对称轴为x=-3 | ||
| C. | 其最大值为1 | D. | 当x<3时,y随x的增大而减小 |
7.如果用-10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
| A. | 减少12% | B. | 增加12% | C. | 减少22% | D. | 增加2% |
 正方形ABCD,∠DEA=15°.ED=EC,求证:△DEC为等边三角形.
正方形ABCD,∠DEA=15°.ED=EC,求证:△DEC为等边三角形.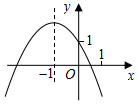 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论: