题目内容
13.(1)$\sqrt{8}×\sqrt{\frac{1}{2}}+{(\sqrt{2})^0}$(2)$(\sqrt{48}-4\sqrt{\frac{1}{8}})-(3\sqrt{\frac{1}{3}}-2\sqrt{0.5})$
(3)$({2\sqrt{48}-3\sqrt{27}})÷\sqrt{6}$
(4)$\sqrt{18}-(\sqrt{2}-1{)^2}+(\sqrt{3}+1)(\sqrt{3}-1)$.
分析 (1)原式利用二次根式乘法法则,以及零指数幂法则计算即可得到结果;
(2)原式去括号化简后,合并即可得到结果;
(3)原式利用二次根式的除法法则计算即可得到结果;
(4)原式利用完全平方公式,平方差公式化简,合并即可得到结果.
解答 解:(1)原式=2+1=3;
(2)原式=4$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$=3$\sqrt{3}$;
(3)原式=2$\sqrt{8}$-3$\sqrt{\frac{9}{2}}$=4$\sqrt{2}$-$\frac{9\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{2}$;
(4)原式=3$\sqrt{2}$-2+2$\sqrt{2}$-1+3-1=5$\sqrt{2}$-1.
点评 此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.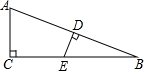 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
5.下列说法正确的是( )
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 互相垂直的直线一定相交 | |
| C. | 从直线外一点到这条直线的垂线段叫做点到直线的距离 | |
| D. | 直线L外一点P与直线L上各点连接而成的线段中最短线段的长度是3cm,则点P到直线L的距离是3cm. |
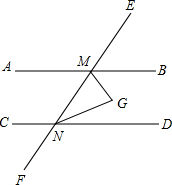 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,则∠G=90°.
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,则∠G=90°.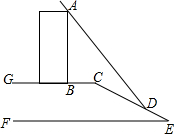 如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)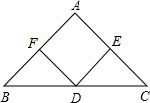 如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,使四边形AFDE为菱形,应添加的条件是AF=AE(添加一个条件即可).
如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,使四边形AFDE为菱形,应添加的条件是AF=AE(添加一个条件即可).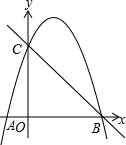 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.