题目内容
6.计算:①$2sin60°-\frac{1}{{\sqrt{3}-2}}$
②$(\sqrt{18}-2\sqrt{24})$÷$\sqrt{3}$-4$\sqrt{\frac{1}{8}}$×$\sqrt{3}$.
分析 ①利用特殊角的三角函数值和分母有理化得到原式=2×$\frac{\sqrt{3}}{2}$+2+$\sqrt{3}$,如果合并即可;
②先进行二次根式的除法和乘法运算,然后合并即可.
解答 解:①原式=2×$\frac{\sqrt{3}}{2}$+$\frac{1}{2-\sqrt{3}}$
=$\sqrt{3}$+2+$\sqrt{3}$
=2$\sqrt{3}$+2;
②原式=$\sqrt{18÷3}$-2$\sqrt{24÷3}$-$\sqrt{2}$×$\sqrt{3}$
=$\sqrt{6}$-4$\sqrt{2}$-$\sqrt{6}$
=-4$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了特殊角的三角函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列命题中,属于真命题的是( )
| A. | 若a>b,则ac>bc | B. | $\sqrt{a^2}$=a(a是实数) | ||
| C. | 三角形的三条中线相交于同一点 | D. | 内错角相等 |
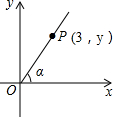 如图,直角坐标系中,P(3,y)是第一象限内的点,且$tanα=\frac{4}{3}$,求sinα.
如图,直角坐标系中,P(3,y)是第一象限内的点,且$tanα=\frac{4}{3}$,求sinα.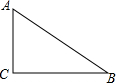 如图,在Rt△ABC中,∠ACB=90°.AC=3,cosB=$\frac{4}{5}$
如图,在Rt△ABC中,∠ACB=90°.AC=3,cosB=$\frac{4}{5}$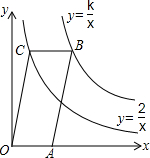 如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.
如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.