题目内容
18.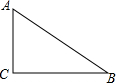 如图,在Rt△ABC中,∠ACB=90°.AC=3,cosB=$\frac{4}{5}$
如图,在Rt△ABC中,∠ACB=90°.AC=3,cosB=$\frac{4}{5}$(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,证明你的结论,并求出OC的长.
分析 (1)首先利用角平分线的作法得出BO,进而以点O为圆心,OC为半径作⊙O即可;
(2)利用角平分线的性质以及直线与圆的位置关系进而求出即可.
解答 解:(1)如图所示: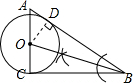 ;
;
(2)相切;过O点作OD⊥AB于D点,
∵BO平分∠ABC,
∴OC=OD,即d=r,
∴⊙O与直线AB相切,
∵∠ACB=90°,AC=3,$cosB=\frac{4}{5}$,
∴BC=4,AB=5.
∵∠A=∠A,∠ADC=∠C,
∴△AOD∽△ABC,
∴$\frac{r}{4}=\frac{3-r}{5}$,$r=\frac{4}{3}$,即OC=$\frac{4}{3}$.
点评 此题主要考查了复杂作图以及角平分线的性质与作法和直线与圆的位置关系,正确利用角平分线的性质求出是解题关键.

练习册系列答案
相关题目
10.计算$\root{3}{64}$的结果是( )
| A. | 8 | B. | -4 | C. | 4 | D. | ±4 |
 如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.
如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.
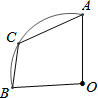 如图,在扇形OAB中,∠AOB=90°,点C在$\widehat{AB}$上,若BC=4,AC=5$\sqrt{2}$,则扇形OAB的面积为$\frac{53π}{4}$.
如图,在扇形OAB中,∠AOB=90°,点C在$\widehat{AB}$上,若BC=4,AC=5$\sqrt{2}$,则扇形OAB的面积为$\frac{53π}{4}$.