题目内容
1．
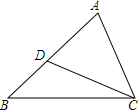如图，∠B=∠ACD，S△ABC：S△ACD=2：1，则AC：AB=$\frac{\sqrt{2}}{2}$．
分析 根据∠B=∠ACD，∠A=∠A，证得△ACD∽△ABC，由相似三角形的性质即可得到结论．
解答 解：∵∠B=∠ACD，∠A=∠A，
∴△ACD∽△ABC，
∴S△ABC：S△ACD=（$\frac{AB}{AC}$）2=2：1，
∴AC：AB=$\frac{\sqrt{2}}{2}$．
故答案为：$\frac{\sqrt{2}}{2}$．
点评 此题考查了相似三角形的判定与性质．此题难度不大，解题的关键是找准对应边．
练习册系列答案
相关题目
11．一钝角三角形的钝角为120°，则其两锐角的角平分线相交所夹的钝角为（ ）
| A． | 120° | B． | 135° | C． | 145° | D． | 150° |
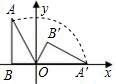如图，在Rt△ABO中，∠B=90°，∠A=30°，OB=2，现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置．求：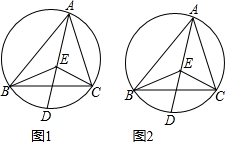
如图，⊙O分别切PA、PB、CE于A、B、D三点，若△PCE的周长为18cm，求AP的长．