题目内容
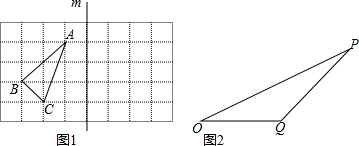
9.在同一直角坐标系中,图①的解析式为y=-x+3(1≤x≤2),图②的解析式为y=$\frac{2}{x}$(1≤x≤2),图③与图②是关于图①对称,则图③的解析式为y=$\frac{2}{x-3}$+3 (1≤x≤2).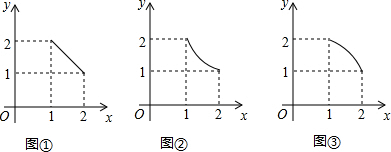
分析 根据坐标变换,可得x′o′y′平面直角坐标系内函数解析式,再根据坐标平移公式,可得答案.
解答 解:由题意,得以(3,3)为原点建立平面直角坐标系x′O′y′,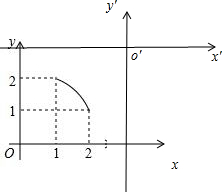 ,
,
图③在此坐标系的解析式为y′=$\frac{2}{x′}$,(-3≤x≤-1),
∵h=3,k=3,
∴由坐标平移公式,得
x=x′+3,y=y′+3,
∴x′=x-3,y′=y-3,
y-3=$\frac{2}{x-3}$,即y=$\frac{2}{x-3}$+3 (1≤x≤2),
故答案为:y=$\frac{2}{x-3}$+3 (1≤x≤2).
点评 本题考查了一次函数图象与几何变换,建立新平面直角坐标系得出函数解析式是解题关键.

练习册系列答案
相关题目
20.下列各数中,无理数是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{9}$ | C. | π | D. | $\root{3}{8}$ |
4.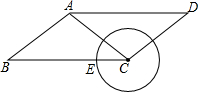 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 0<CE<3或5<CE≤8 | D. | 3<CE≤5 |
14.下列命题,正确的是( )
| A. | 所有正方形都全等 | |
| B. | 等腰梯形的对角线互相平分 | |
| C. | 相等的圆周角所对的弧相等 | |
| D. | 顺次连结四边形各边中点所得到的四边形是平行四边形 |
1.已知5x-4y-7z=0,4x-3y-6z=0,则x:y:z为( )
| A. | 3:2:1 | B. | 9:4:1 | C. | 1:2:3 | D. | 1:4:9 |
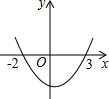 如图,抛物线y=ax2+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax2+bx+c>0的解集是x>3或x<-2.
如图,抛物线y=ax2+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax2+bx+c>0的解集是x>3或x<-2.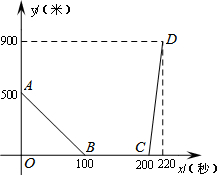 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,