题目内容
在Rt△ABC中,∠ABC=90°,AB=2,BC=3,则AC上的中线长为 .
考点:勾股定理,直角三角形斜边上的中线
专题:
分析:在Rt△ABC中,根据勾股定理可以计算AC的长度,然后由“直角三角形中斜边的中线为斜边长的一半”来求AC上的中线长.
解答: 解:如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=3,BD是AC边上的中线.
解:如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=3,BD是AC边上的中线.
在Rt△ABC中,由勾股定理,得
AC=
=
=
.
又BD是AC边上的中线,
∴BD=
AC=
.
故答案是:
.
 解:如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=3,BD是AC边上的中线.
解:如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=3,BD是AC边上的中线.在Rt△ABC中,由勾股定理,得
AC=
| AB2+BC2 |
| 22+32 |
| 13 |
又BD是AC边上的中线,
∴BD=
| 1 |
| 2 |
| ||
| 2 |
故答案是:
| ||
| 2 |
点评:本题考查了直角三角形中勾股定理的运用,考查了斜边中线长为斜边中线的一半的性质,本题中根据勾股定理计算斜边长是解题的关键.

练习册系列答案
相关题目
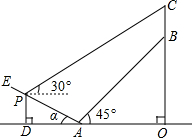 如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=
如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα= 已知△ABC中,AB=8,AC=6,点D是线段AC的中点,点E在线段AB上且△ADE∽△ABC,则AE=
已知△ABC中,AB=8,AC=6,点D是线段AC的中点,点E在线段AB上且△ADE∽△ABC,则AE=