题目内容
11. 如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有3对.
如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有3对.
分析 先利用边角边定理判断△ABD和△ACD全等,再根据全等三角形的对应角相等得到∠B=∠C,∠BAD=∠CAD,然后利用角角边定理即可判定△BDE≌△CDF,△ADE≌△ADF.
解答 解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
∵$\left\{\begin{array}{l}{AD=DA}\\{∠ADB=∠ADC}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD(SAS);
∴∠B=∠C,∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠AED=∠AFD=∠CFD=90°,
∴△BDE≌△CDF,△ADE≌△ADF.
全等三角形有3对;
故答案为3.
点评 本题主要考查全等三角形的判定,先证明△ABD和△ACD全等是解本题的突破点,寻找时要由易到难,逐步深入,做到不重不漏.

练习册系列答案
相关题目
1. 如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是( )
如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是( )
 如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是( )
如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是( )| A. | 89° | B. | 91° | C. | 92° | D. | 90° |
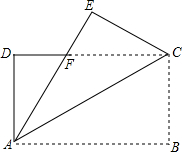 如图,在长方形纸片ABCD中,AB=18,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,求AD的长.
如图,在长方形纸片ABCD中,AB=18,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,求AD的长.