题目内容
3.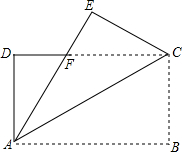 如图,在长方形纸片ABCD中,AB=18,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,求AD的长.
如图,在长方形纸片ABCD中,AB=18,把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=13,求AD的长.
分析 由折叠得:∠EAC=∠BAC,AE=AB=18,根据平行线性质得:AF=FC=13,再求出EF=5,利用勾股定理求出EC的长,即AD的长.
解答 解:由折叠得:∠EAC=∠BAC,AE=AB=18,
∵四边形ABCD为长方形,
∴DC∥AB,
∴∠DCA=∠BAC,
∴∠EAC=∠DCA,
∴FC=AF=13,
∵AB=18,AF=13,
∴EF=18-13=5,
∵∠E=∠B=90°,
∴EC=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∵AD=BC=EC,
∴AD=12.
点评 本题是折叠问题,考查了长方形、折叠的性质,难度不大;属于常考题型,熟练掌握折叠前后的两个对应角相等;与平行线的内错角相等得出等腰三角形,根据等角对等边,求出边的长,利用勾股定理解决问题.

练习册系列答案
相关题目
 如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有3对.
如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有3对.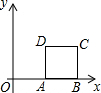 如图,在平面直角坐标系中,已知A(1,0),B(2,0),四边形ABCD是正方形.
如图,在平面直角坐标系中,已知A(1,0),B(2,0),四边形ABCD是正方形.