题目内容
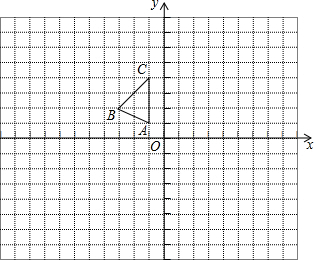
1. 如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是( )
如图,CO⊥AB,DO是∠AOC的平分线,EO是∠BOC的平分线,则∠DOE的度数是( )| A. | 89° | B. | 91° | C. | 92° | D. | 90° |
分析 根据OD是∠AOC的角平分线,OE是∠BOC的平分线可得∠DOC=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,又根据∠DOE=∠DOC+∠COE,可求得∠DOE=$\frac{1}{2}$∠AOB=90°.
解答 解:∵OD是∠AOC的角平分线,OE是∠BOC的平分线,
∴∠DOC=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,
∵∠DOE=∠DOC+∠COE,
∴∠DOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB=90°.
故选D.
点评 本题考查了余角和补角以及角平分线的定义,解答本题的关键是掌握互余两角和为90°.

练习册系列答案
相关题目
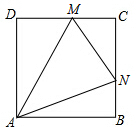 点M、N分别在正方形ABCD的边CD、BC上,已知△MCN的周长等于正方形ABCD周长的一半,求∠MAN的度数.
点M、N分别在正方形ABCD的边CD、BC上,已知△MCN的周长等于正方形ABCD周长的一半,求∠MAN的度数. 如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有3对.
如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有3对.