题目内容
15．先化简，再求代数式：（$\frac{1}{x-y}$-$\frac{2}{{x}^{2}-xy}$）÷$\frac{x-2}{3x}$的值，其中x=2+tan60°，y=4sin30°．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x与y的值代入计算即可求出值．
解答 解：原式=$\frac{x-2}{x（x-y）}$•$\frac{3x}{x-2}$=$\frac{3}{x-y}$，
当x=2+$\sqrt{3}$，y=4×$\frac{1}{2}$=2时，原式=$\sqrt{3}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
5．
如图是一张边长为8的正方形纸片，在正方形纸片上剪下一个腰长为5的等腰三角形（要求：等腰三角形的一个顶点与正方形的一个顶点重合，其余两个顶点在正方形的边上），则剪下的等腰三角形的底边长是（ ）
如图是一张边长为8的正方形纸片，在正方形纸片上剪下一个腰长为5的等腰三角形（要求：等腰三角形的一个顶点与正方形的一个顶点重合，其余两个顶点在正方形的边上），则剪下的等腰三角形的底边长是（ ）| A． | 4$\sqrt{3}$ | B． | 5$\sqrt{2}$ | C． | 4$\sqrt{3}$或5$\sqrt{2}$ | D． | 4$\sqrt{5}$或5$\sqrt{2}$ |
6．已知数据：2，4，2，5，7．则这组数据的众数和中位数分别是（ ）
| A． | 2，2 | B． | 2，4 | C． | 2，5 | D． | 4，4 |
3．
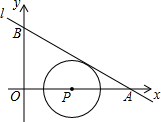我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
10．
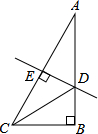如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD．若BD=1，则AC的长是（ ）
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD．若BD=1，则AC的长是（ ）| A． | 2$\sqrt{3}$ | B． | 2 | C． | 4$\sqrt{3}$ | D． | 4 |
20．使$\sqrt{x-1}$有意义的x的取值范围是（ ）
| A． | x≠1 | B． | x≥1 | C． | x＞1 | D． | x≥0 |
如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA=125°．
如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为5．