题目内容
12．（1）解方程：x2-2x-3=0；（2）解不等式组：$\left\{\begin{array}{l}x-1＞2\\ x+2＜4x-1\end{array}$．
分析 （1）将方程的左边因式分解后即可求得方程的解；
（2）分别求得两个不等式解集后取其公共部分即可求得不等式组的解集．
解答 解：（1）因式分解得：（x+1）（x-3）=0，
即x+1=0或x-3=0，
解得：x1=-1，x2=3；
（2）$\left\{\begin{array}{l}x-1＞2①\\ x+2＜4x-1②\end{array}$
由①得x＞3
由②得x＞1
∴不等式组的解集为x＞3．
点评 本题考查了因式分解法解一元二次方程及解一元一次不等式组的知识，属于基础知识，难度不大．
练习册系列答案
相关题目
2．
如图所示，AH∥DG∥BC，DF∥AC，图中和∠ACB相等的角（不包括自身）有（ ）
如图所示，AH∥DG∥BC，DF∥AC，图中和∠ACB相等的角（不包括自身）有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
3．
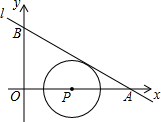我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
20．使$\sqrt{x-1}$有意义的x的取值范围是（ ）
| A． | x≠1 | B． | x≥1 | C． | x＞1 | D． | x≥0 |
如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA=125°．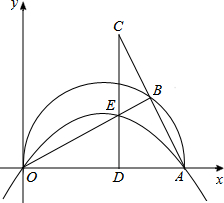
如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D，交线段OB于点E，已知CD=8，抛物线经过O、E、A三点．
如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为5．
如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．