题目内容
 已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上.
已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上.(1)用含有a的式子表示顶点M的坐标,并求出抛物线C2的函数解析式;
(2)若抛物线C2的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F,且满足EF=
| 1 |
| 2 |
(3)若P是抛物线C2对称轴上使△ABC的周长取得最小值的点,过点P任意作一条与y不平行的直线l交抛物线于M、N两点,当y轴平分MN时,求直线l的函数解析式.
考点:二次函数综合题
专题:
分析:(1)利用配方法将y=x2+2ax+2x-a+1改写成y=(x+a+1)2-a2-3a,求出顶点M的坐标是(-a-1,-a2-3a);求抛物线C2的函数解析式有两种方法.方法一:分别取a=0,-1,1,得到三个顶点坐标是M1(-1,0)、M2(0,2)、M3(-2,-4),利用待定系数法可求出抛物线C2的函数解析式;方法二:令-a-1=x,将a=-x-1代入y=-a2-3a,即可求出抛物线C2的函数解析式;
(2)分两种情况:①当点E在x轴上方时,过点E作EH⊥x轴于点H.由△CAO∽△EFH,根据相似三角形对应边成比例得出EH=
CO=1,解方程-x2+x+2=1求出x的值,得到E点坐标;②当点E在x轴下方时,同理可求得E点坐标;
(3)要使△ACP的周长最小,只需AP+CP最小即可.连接BC交对称轴于P点,因为点A、B关于x=
对称,根据轴对称性质以及两点之间线段最短,可知此时AP+CP最小.运用待定系数法求出直线BC解析式为y=-x+2,将x=
代入,求出y=
,得到P(
,
).再令经过点P(
,
)的直线l为y=kx-
k+
,设M(x1,y1),N(x2,y2),将y=kx-
k+
与y=-x2+x+2,联立化简得出x2+(k-1)x-
(k+1)=0,当x1+x2=1-k=0时,y轴平分MN,由此求出k=1,得到直线l:y=x+1.
(2)分两种情况:①当点E在x轴上方时,过点E作EH⊥x轴于点H.由△CAO∽△EFH,根据相似三角形对应边成比例得出EH=
| 1 |
| 2 |
(3)要使△ACP的周长最小,只需AP+CP最小即可.连接BC交对称轴于P点,因为点A、B关于x=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵y=x2+2ax+2x-a+1=x2+(2a+2)x-a+1=(x+a+1)2-a2-3a,
∴顶点M的坐标是(-a-1,-a2-3a).
方法一:分别取a=0,-1,1,得到三个顶点坐标是M1(-1,0)、M2(0,2)、M3(-2,-4),
过这三个顶点的二次函数的表达式是y=-x2+x+2.
将顶点坐标M(-a-1,-a2-3a)代入y=-x2+x+2的左右两边,
得左边=-a2-3a,右边=-(-a-1)2+(-a-1)+2=-a2-3a,
∴左边=右边.
即无论a取何值,顶点M都在抛物线y=-x2+x+2上.
即所求抛物线的函数表达式是C2:y=-x2+x+2;
方法二:令-a-1=x,将a=-x-1代入y=-a2-3a,得y=-(-x-1)2-3(-x-1)=-x2+x+2,
 即所求抛物线的函数表达式是C2:y=-x2+x+2;
即所求抛物线的函数表达式是C2:y=-x2+x+2;
(2)分两种情况:
①当点E在x轴上方时,过点E作EH⊥x轴于点H.
∵AC∥EF,
∴△CAO∽△EFH,
=
=2,
∴EH=
CO=
×2=1,即E点纵坐标为1,
当y=1时,-x2+x+2=1,
解得x=
或x
(舍去),
∴E(
,1);
②当点E在x轴下方时,同理可求得E(
,-1);
综上所述,满足条件的E点坐标有两个:E(
,1)或 (
(
,-1);
(3)连接BC交对称轴于P点.
∵点A、B关于x=
对称,
∴PB=PA,
∴AP+CP=BP+CP=BC最小,△ACP的周长=AC+AP+CP=
+BC最小.
∵B(2,0),C(0,2),
∴直线BC解析式为y=-x+2,
∴当x=
时,y=-
+2=
,
∴P(
,
).
令经过点P(
,
)的直线l为y=kx-
k+
,
设M(x1,y1),N(x2,y2),
∵y=kx-
k+
,y=-x2+x+2,
联立化简得:x2+(k-1)x-
(k+1)=0,
∴当x1+x2=1-k=0时,y轴平分MN,
解得k=1,
∴直线l的函数解析式为y=x+1.
∴顶点M的坐标是(-a-1,-a2-3a).
方法一:分别取a=0,-1,1,得到三个顶点坐标是M1(-1,0)、M2(0,2)、M3(-2,-4),
过这三个顶点的二次函数的表达式是y=-x2+x+2.
将顶点坐标M(-a-1,-a2-3a)代入y=-x2+x+2的左右两边,
得左边=-a2-3a,右边=-(-a-1)2+(-a-1)+2=-a2-3a,
∴左边=右边.
即无论a取何值,顶点M都在抛物线y=-x2+x+2上.
即所求抛物线的函数表达式是C2:y=-x2+x+2;
方法二:令-a-1=x,将a=-x-1代入y=-a2-3a,得y=-(-x-1)2-3(-x-1)=-x2+x+2,
 即所求抛物线的函数表达式是C2:y=-x2+x+2;
即所求抛物线的函数表达式是C2:y=-x2+x+2;(2)分两种情况:
①当点E在x轴上方时,过点E作EH⊥x轴于点H.
∵AC∥EF,
∴△CAO∽△EFH,
| CO |
| EH |
| AC |
| EF |
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
当y=1时,-x2+x+2=1,
解得x=
| ||
| 2 |
1-
| ||
| 2 |
∴E(
1+
| ||
| 2 |
②当点E在x轴下方时,同理可求得E(
1+
| ||
| 2 |
综上所述,满足条件的E点坐标有两个:E(
1+
| ||
| 2 |
 (
(1+
| ||
| 2 |
(3)连接BC交对称轴于P点.
∵点A、B关于x=
| 1 |
| 2 |
∴PB=PA,
∴AP+CP=BP+CP=BC最小,△ACP的周长=AC+AP+CP=
| 10 |
∵B(2,0),C(0,2),
∴直线BC解析式为y=-x+2,
∴当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴P(
| 1 |
| 2 |
| 3 |
| 2 |
令经过点P(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
设M(x1,y1),N(x2,y2),
∵y=kx-
| 1 |
| 2 |
| 3 |
| 2 |
联立化简得:x2+(k-1)x-
| 1 |
| 2 |
∴当x1+x2=1-k=0时,y轴平分MN,
解得k=1,
∴直线l的函数解析式为y=x+1.
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点坐标求法,运用待定系数法求二次函数、一次函数的解析式,相似三角形的判定与性质,轴对称的性质.综合性较强,有一定难度.运用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
相关题目
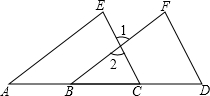 (1)如图,点A、B、C、D在一条直线上,填写下列空格:
(1)如图,点A、B、C、D在一条直线上,填写下列空格: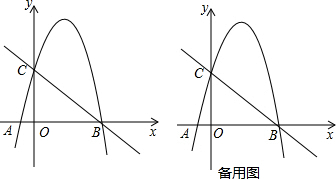
 如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需要增加一个条件,这个条件可以是:
如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需要增加一个条件,这个条件可以是: