题目内容
已知抛物线y=-3x2+12x-8
(1)用配方法求它的解析式;
(2)求它与x轴和与y轴的交点坐标;
(3)当x为何值时,y有最大值或最小值.
(1)用配方法求它的解析式;
(2)求它与x轴和与y轴的交点坐标;
(3)当x为何值时,y有最大值或最小值.
考点:二次函数的三种形式,二次函数的最值,抛物线与x轴的交点
专题:
分析:(1)根据配方法的操作整理即可;
(2)令y=0,解关于x的一元二次方程求出与y轴的交点坐标,令x=0求解得到与y轴的交点坐标;
(3)根据二次函数的最值问题解答.
(2)令y=0,解关于x的一元二次方程求出与y轴的交点坐标,令x=0求解得到与y轴的交点坐标;
(3)根据二次函数的最值问题解答.
解答:解:(1)y=-3x2+12x-8
=-3(x2-4x+4)+12-8
=-3(x-2)2+4;
(2)令y=0,则-3x2+12x-8=0,
△=122-4×(-3)×(-8)=144-96=48,
所以,x1=
,x2=
,
所以,与x轴的交点坐标为(
,0)和(
,0),
令x=0,则y=-8,
所以与y轴的交点坐标为(0,-8);
(3)∵a=-3<0,
∴x=2时,y有最大值4.
=-3(x2-4x+4)+12-8
=-3(x-2)2+4;
(2)令y=0,则-3x2+12x-8=0,
△=122-4×(-3)×(-8)=144-96=48,
所以,x1=
6+2
| ||
| 3 |
6-2
| ||
| 3 |
所以,与x轴的交点坐标为(
6+2
| ||
| 3 |
6-2
| ||
| 3 |
令x=0,则y=-8,
所以与y轴的交点坐标为(0,-8);
(3)∵a=-3<0,
∴x=2时,y有最大值4.
点评:本题考查了二次函数的三种形式的转化,二次函数的最值问题,抛物线与x轴的交点,熟练掌握配方法的操作以及与坐标轴的交点的求法是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
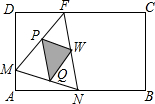 如图,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动,当动点N运动到点A时,M、N两点同时停止运动.连结FM、MN、FN,当F、N、M不在同一条直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
如图,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动,当动点N运动到点A时,M、N两点同时停止运动.连结FM、MN、FN,当F、N、M不在同一条直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题: 在图中,将大写字母A绕它上侧的顶点按逆时针方向旋转90°,作出旋转后的图案,同时作出字母A向左平移5个单位的图象.
在图中,将大写字母A绕它上侧的顶点按逆时针方向旋转90°,作出旋转后的图案,同时作出字母A向左平移5个单位的图象. 已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上.
已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上.