题目内容
12.某班学生的期中成绩(成绩为整数)的频数分布表如下,请根据表中提供的信息回答下列问题:| 分组 | 频数 | 频率 |
| 49.5-59.5 | 3 | 0.05 |
| 59.5-69.5 | 9 | m |
| 69.5-79.5 | n | 0.40 |
| 79.5-89.5 | 18 | 0.30 |
| 89.5-99.5 | 6 | p |
| 合计 | q | 1.0 |
(2)在表内,频率最小的一组的成绩范围是49.5-59.5.
(3)成绩优秀的学生有24人(成绩大于或等于80分为优秀).
分析 (1)根据频数除以频率,可得总人数q;根据频数除以总数,可得m;再根据各组人数,可得n;根据根据频数除以总数,可得p;
(2)由各组的频率大小,进相比较即可得到结论;
(3)根据最后两组的人数,即可得到成绩优秀的学生数量.
解答 解:(1)∵总人数q=3÷0.05=60(人),
∴m=9÷60=0.15,
n=60-3-9-18-6=24(人),
p=6÷60=0.1,
故答案为:0.15,24,0.1,60;
(2)由各组的频率可知,频率最小的一组的成绩范围是49.5-59.5,
故答案为:49.5-59.5;
(3)成绩优秀的学生有18+6=24(人).
故答案为:24.
点评 本题主要考查了频数分布表,在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.某商店4、5月份出售同一品牌的各种规格的空调,销售台数如下表所示:
根据上表回答:
(1)该商店平均每月销售空调多少台?
(2)在研究6月份进货时,商店经理会根据4、5月份的销售情况做出什么决定?
 | 1匹 | 1.2匹 | 1.5匹 | 2匹 |
| 4 | 12 | 20 | 9 | 4 |
| 5 | 16 | 30 | 14 | 8 |
(1)该商店平均每月销售空调多少台?
(2)在研究6月份进货时,商店经理会根据4、5月份的销售情况做出什么决定?
7.已知$\frac{a}{5}$=$\frac{b}{3}$=k(k≠0),则$\frac{a-b}{a+b}$=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
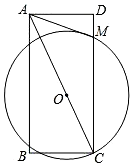 如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.
如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.