题目内容
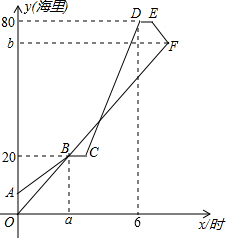 在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.
在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.(1)求a的值;
(2)乙船出发多长时间与甲船相遇?
(3)求b的值;
(4)请直接写出在两船第三次相遇前,两船相距10海里时的所有x的值.
考点:一次函数的应用
专题:
分析:(1)由图可知,两船第一次在点B(a,20)相遇,因为乙的速度为10海里/时,根据时间=路程÷速度即可求解;
(2)由图可知,两个函数图象的交点有3个,所以两船相遇有三次,第一次:在B点相遇,此时时间为2时;第二次:在BF与CD的交点相遇.先利用待定系数法求出CD的解析式为y=20x-40,OF的解析式为y=10x,把y=20x-40代入y=10x,求出x的值为第二次相遇的时间;第三次相遇在F点,则时间为7+(80-70)÷(20+10)=7时20分;
(3)把F点的横坐标代入乙的解析式即可求出b的值;
(4)由图可知,当x≤2时,由于乙船的速度大于甲船的速度,而x=0时,甲在乙前面5海里,所以x≤2时两船不可能相距10海里;当2<x≤3时,甲船因故障维修,距离港口20海里,乙船距离港口10x海里,由10x-20=10,解得x=3;当3<x≤6时,甲船追上乙船并且超出乙船10海里,由(20x-40)-10x=10,解得x=5;当6<x≤7时,甲船距离港口80海里,在目的地救援,乙船距离港口10x海里,由80-10x=10,解得x=7.
(2)由图可知,两个函数图象的交点有3个,所以两船相遇有三次,第一次:在B点相遇,此时时间为2时;第二次:在BF与CD的交点相遇.先利用待定系数法求出CD的解析式为y=20x-40,OF的解析式为y=10x,把y=20x-40代入y=10x,求出x的值为第二次相遇的时间;第三次相遇在F点,则时间为7+(80-70)÷(20+10)=7时20分;
(3)把F点的横坐标代入乙的解析式即可求出b的值;
(4)由图可知,当x≤2时,由于乙船的速度大于甲船的速度,而x=0时,甲在乙前面5海里,所以x≤2时两船不可能相距10海里;当2<x≤3时,甲船因故障维修,距离港口20海里,乙船距离港口10x海里,由10x-20=10,解得x=3;当3<x≤6时,甲船追上乙船并且超出乙船10海里,由(20x-40)-10x=10,解得x=5;当6<x≤7时,甲船距离港口80海里,在目的地救援,乙船距离港口10x海里,由80-10x=10,解得x=7.
解答:解:(1)∵乙船以10海里/时的速度匀速行驶,a小时行驶20海里,
∴a=20÷10=2(小时);
(2)两船相遇有三次,
第一次:在B点相遇,此时时间为2时;
第二次:在BF与CD的交点相遇.
设直线CD的解析式为y=kx+n,
∵C(3,20),D(6,80),
∴
,
解得
.
∴直线CD的解析式为y=20x-40,
∵直线OF的解析式为y=10x,
把y=20x-40代入y=10x,得20x-40=10x,解得x=4,
所以第二次相遇的时间为4时;
第三次相遇在F点.
∵E点横坐标为7,
∴当x=7时,y=10x=70,
∴甲船原路匀速返回与乙船相遇需要的时间为(80-70)÷(20+10)=
小时=20分钟,
∴第三次相遇的时间7时+
时=7时20分;
(3)当x=7
时,b=10x=
=73
;
(4)在两船第三次相遇前,两船相距10海里时x的值为3,5,7.
∴a=20÷10=2(小时);
(2)两船相遇有三次,
第一次:在B点相遇,此时时间为2时;
第二次:在BF与CD的交点相遇.
设直线CD的解析式为y=kx+n,
∵C(3,20),D(6,80),
∴
|
解得
|
∴直线CD的解析式为y=20x-40,
∵直线OF的解析式为y=10x,
把y=20x-40代入y=10x,得20x-40=10x,解得x=4,
所以第二次相遇的时间为4时;
第三次相遇在F点.
∵E点横坐标为7,
∴当x=7时,y=10x=70,
∴甲船原路匀速返回与乙船相遇需要的时间为(80-70)÷(20+10)=
| 1 |
| 3 |
∴第三次相遇的时间7时+
| 1 |
| 3 |
(3)当x=7
| 1 |
| 3 |
| 220 |
| 3 |
| 1 |
| 3 |
(4)在两船第三次相遇前,两船相距10海里时x的值为3,5,7.
点评:本题考查了一次函数的应用,待定系数法求一次函数的解析式,路程、速度与时间之间的关系,两函数交点坐标的求法,难度适中.从图中获取有用信息是解题的关键.

练习册系列答案
相关题目
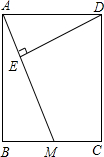 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.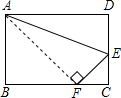 如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=
如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=