题目内容
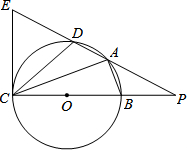 如图,已知BC为⊙O的直径,EC是⊙O的切线,C是切点,EP交⊙O于点A,D,交CB延长线于点P.连接CD,CA,AB.
如图,已知BC为⊙O的直径,EC是⊙O的切线,C是切点,EP交⊙O于点A,D,交CB延长线于点P.连接CD,CA,AB.(1)求证:∠ECD=∠EAC;
(2)若PB=OB=2,CD=3,求PA的长.
考点:切线的性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)如图1,连接OD.利用弦切角定理和圆周角定理可以证得结论;
(2)如图2,连接BD,过点D作DF⊥BC于点F.通过相似三角形△PAB∽△PCD的对应边成比例知
=
.把相关线段的长度代入可以得到:PA=2
.
(2)如图2,连接BD,过点D作DF⊥BC于点F.通过相似三角形△PAB∽△PCD的对应边成比例知
| PA |
| PC |
| PB |
| PD |
| 2 |
解答: (1)证明:如图1,连接OD.
(1)证明:如图1,连接OD.
∵EC是⊙O的切线,CD是⊙O的弦,
∴∠ECD=
∠COD(弦切角的度数等于它所夹的弧的圆心角的度数的一半).
又∵∠DAC=
∠COD(在同圆中,同弧所对的圆周角是所对的圆心角的一半),
∴∠ECD=∠DAC,即∠ECD=∠EAC;
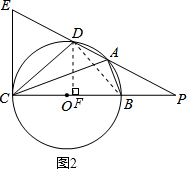
(2)解:如图2,连接BD,过点D作DF⊥BC于点F.
∵BC是⊙O的直径,∴∠CDB=90°.
∴在Rt△CDB中,BD=
=
,DF=
=
.
在Rt△CDF中,CF=
=
.
∴PF=PC-CF=
.
在Rt△DFP中,DP=
=3
.
∵∠PAB=∠PCD,∠P=∠P,
∴△PAB∽△PCD.
∴
=
.
∴
=
.
∴PA=2
.
 (1)证明:如图1,连接OD.
(1)证明:如图1,连接OD.∵EC是⊙O的切线,CD是⊙O的弦,
∴∠ECD=
| 1 |
| 2 |
又∵∠DAC=
| 1 |
| 2 |
∴∠ECD=∠DAC,即∠ECD=∠EAC;
(2)解:如图2,连接BD,过点D作DF⊥BC于点F.
∵BC是⊙O的直径,∴∠CDB=90°.
∴在Rt△CDB中,BD=
| BC2-CD2 |
| 7 |
| CD•BD |
| BC |
3
| ||
| 4 |

在Rt△CDF中,CF=
| CD2-DF2 |
| 9 |
| 4 |
∴PF=PC-CF=
| 15 |
| 4 |
在Rt△DFP中,DP=
| DF2+PF2 |
| 2 |
∵∠PAB=∠PCD,∠P=∠P,
∴△PAB∽△PCD.
∴
| PA |
| PC |
| PB |
| PD |
∴
| PA |
| 6 |
| 2 | ||
3
|
∴PA=2
| 2 |
点评:本题考查了切线的性质、勾股定理以及相似三角形的判定与性质.解题过程中,利用了弦切角定理和圆内接四边形的性质.注意,圆的知识的综合运用.

练习册系列答案
相关题目
直角三角形的斜边比一直角边长2cm,另一直角边长为6cm,则它的斜边长( )
| A、4cm | B、8cm |
| C、10cm | D、12cm |
 如图,
如图,
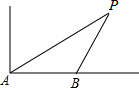 如图,海中有一个小岛P,它的周围25海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行30海里到达B点,此时测得小岛P在北偏东30°方向上.
如图,海中有一个小岛P,它的周围25海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行30海里到达B点,此时测得小岛P在北偏东30°方向上. 已知:如图,C是AE上一点,∠B=∠DAE,BC∥DE,AC=DE.
已知:如图,C是AE上一点,∠B=∠DAE,BC∥DE,AC=DE.