题目内容
5.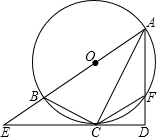 如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC.
如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC.(1)求证:BC=CF;
(2)若AD=6,DE=8,求CD的长.
(3)试探究AB,AF,DF之间的数量关系,并证明你的结论.
分析 (1)根据切线的性质首先得出CO⊥ED,再利用平行线的判定得出CO∥AD,进而利用圆周角、圆心角定理得出BC=CF;
(2)首先求出△EOC∽△EAD,由相似三角形的性质可知:$\frac{EO}{EA}=\frac{OC}{AD}$=$\frac{EC}{ED}$,设⊙O的半径为r,则OE=10-r,进而得出r的长,然后可求得EC的长,从而得到CD的长;
(3)利用全等三角形的判定得出Rt△AGC≌Rt△ADC,进而得出Rt△CGB≌Rt△CDF,即可求出AD+DF=AB得出答案即可.
解答 (1)证明:如图1所示:连接OC.
∵ED切⊙O于点C,
∴CO⊥ED.
∵AD⊥EC,
∴CO∥AD.
∴∠OCA=∠CAD.
∵∠OCA=∠OAC,
∴∠OAC=∠CAD.
∴$\widehat{BC}=\widehat{CF}$.
∴BC=CF.
(2)解:如图1所示:
∵在Rt△ADE中,AD=6,DE=8,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=10.
∵CO∥AD,
∴△EOC∽△EAD.
∴$\frac{EO}{EA}=\frac{OC}{AD}$=$\frac{EC}{ED}$.
设⊙O的半径为r,则OE=10-r,
∴$\frac{10-r}{10}=\frac{r}{6}$.
∴r=$\frac{15}{4}$.
∴$\frac{\frac{15}{4}}{6}=\frac{EC}{8}$.
∴EC=5.
∴CD=3.
(3)AF+2DF=AB.
理由:过C作CG⊥AB于G,连接OC.
∵∠OAC=∠CAD,AD⊥EC,
∴CG=CD,
在Rt△AGC和Rt△ADC中,
$\left\{\begin{array}{l}{CG=CD}\\{AC=AC}\end{array}\right.$,
∴Rt△AGC≌Rt△ADC(HL).
∴AG=AD,
在Rt△CGB和Rt△CDF中,
$\left\{\begin{array}{l}{BC=FC}\\{CG=CD}\end{array}\right.$,
∴Rt△CGB≌Rt△CDF(HL),
∴GB=DF.
∵AG+GB=AB,
∴AD+DF=AB.
∴AF+DF+DF=AB.
∴AF+2DF=AB.
点评 此题主要考查了切线的性质定理和圆周角及弧的关系、相似三角形的判定与性质、全等三角形的判定与性质等知识,得出GB=DF是解题关键.

| A. | -5÷$\frac{1}{5}$×5=-5 | B. | 2a+3b=5ab | C. | 7ab-3ab=4 | D. | x2y-2x2y=-x2y |
 如图,在⊙O中,CD⊥AB于点D,求证:∠ACD=∠BCD.
如图,在⊙O中,CD⊥AB于点D,求证:∠ACD=∠BCD. 如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为9.
如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为9. 如图中,∠A+∠B+∠C+∠D+∠F+∠G等于360度.
如图中,∠A+∠B+∠C+∠D+∠F+∠G等于360度.
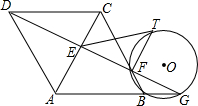 已知:?ABCD过点D作直线交AC于E,交BC于F,交AB的延长线于G,经过B、G、F三点作⊙O,过E作⊙O的切线ET,T为切点.求证:ET=ED.
已知:?ABCD过点D作直线交AC于E,交BC于F,交AB的延长线于G,经过B、G、F三点作⊙O,过E作⊙O的切线ET,T为切点.求证:ET=ED.