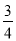题目内容
3.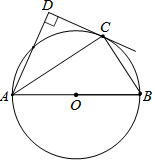 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.(1)求证:AC平分∠DAB;
(2)求证:AC2=AD•AB;
(3)若AD=$\frac{8}{5}$,sinB=$\frac{4}{5}$,求线段BC的长.
分析 (1)连接OC,由OA=OC可以得到∠OAC=∠OCA,证出AD∥OC,由平行线的性质证出∠DAC=∠OCA,即可得出结论;
(2)由圆周角定理证出∠ACB=90°=∠ADC,证明△ADC∽△ACB,得出对应边成比例,即可得出结论;
(3)由相似三角形的性质得出∠ACD=∠B,得出sin∠ACD=$\frac{AD}{AC}$=sinB=$\frac{4}{5}$,求出AC=2,AB=$\frac{5}{2}$,在Rt△ABC中,由勾股定理即可求出BC的长.
解答 (1)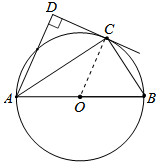 证明:连接OC,如图所示:
证明:连接OC,如图所示:
∵CD切⊙O于C,
∴CO⊥CD,
又∵AD⊥CD,
∴AD∥CO.
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
∴AC平分∠BAD.
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°=∠ADC,
∵∠DAC=∠CAO,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AD•AB;
(3)解:由(2)得:△ADC∽△ACB,
∴∠ACD=∠B,
∴sin∠ACD=$\frac{AD}{AC}$=sinB=$\frac{4}{5}$,
∴AC=$\frac{5}{4}$AD=$\frac{5}{4}$×$\frac{8}{5}$=2,
∵AC2=AD•AB,
∴AB=$\frac{A{C}^{2}}{AD}$=$\frac{{2}^{2}}{\frac{8}{5}}$=$\frac{5}{2}$,
在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\frac{3}{2}$.
点评 此题主要考查了切线的性质、平行线的性质、等腰三角形的性质、相似三角形的判定与性质、三角函数、勾股定理等知识;熟练掌握切线的性质,证明三角形相似是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案 小明和小强分别从A、B两地出发匀速相向而行,达到对方出发地后均立即以原速返回.已知小明到达B地半小时后,小强到达A地.如图表示他们出发时间t(单位:小时)与距离A地的路程S(单位:千米)之间的关系图,则出发后$\frac{45}{11}$小时,小明和小强第2次相遇.
小明和小强分别从A、B两地出发匀速相向而行,达到对方出发地后均立即以原速返回.已知小明到达B地半小时后,小强到达A地.如图表示他们出发时间t(单位:小时)与距离A地的路程S(单位:千米)之间的关系图,则出发后$\frac{45}{11}$小时,小明和小强第2次相遇.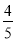 B.
B. 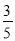 C.
C. 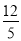 D.
D.