题目内容
11.已知关于x的方程kx2+(2k+1)x+2=0.(1)求证:无论k取任何实数时,方程总有实数根.
(2)是否存在实数k使方程两根的倒数和为2?若存在,请求出k的值;若不存在,请说明理由.
分析 (1)分类讨论:当k=0时,方程变形一元一次方程,有一个实数解;当k≠0时,计算判别式得到△=(2k-1)2,由此得到△≥0,由此判断当k≠0时,方程有两个实数根;
(2)由韦达定理可得x1+x2=-$\frac{2k+1}{k}$,x1x2=$\frac{2}{k}$,令$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=2,建立关于k的方程,解答即可.
解答 解:(1)当k=0时,方程变形为x+2=0,解得x=-2;
当k≠0时,△=(2k+1)2-4•k•2=(2k-1)2,
∵(2k-1)2≥0,
∴△≥0,
∴当k≠0时,方程有实数根,
∴无论k取任何实数时,方程总有实数根;
(2)存在,
设方程两根为x1、x2,
则x1+x2=-$\frac{2k+1}{k}$,x1x2=$\frac{2}{k}$,
∵$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=2,即$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=2,
∴$\frac{-\frac{2k+1}{k}}{\frac{2}{k}}$=2,即-$\frac{2k+1}{2}$=2,
解得:k=-$\frac{5}{2}$,
故存在实数k使方程两根的倒数和为2.
点评 本题考查了根的判别式、一元二次方程的定义、根与系数的关系,当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
2.将161000用科学记数法表示为( )
| A. | 0.161×106 | B. | 1.61×105 | C. | 16.1×104 | D. | 161×103 |
16.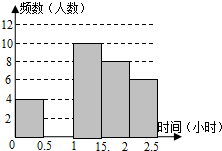 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
(1)在表格中,a=12,b=0.2;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.| 时间(小时) | 频数(人数) | 频率 |
| 0≤t<0.5 | 4 | 0.1 |
| 0.5≤t<1 | a | 0.3 |
| 1≤t<1.5 | 10 | 0.25 |
| 1.5≤t<2 | 8 | b |
| 2≤t<2.5 | 6 | 0.15 |
| 合计 | 1 |
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
3. 如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )
如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )
 如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )
如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC,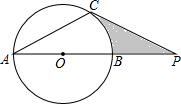 如图,⊙O直径AB与弦AC的夹角∠A=30°,过C点的切线与AB的延长线交于点P.
如图,⊙O直径AB与弦AC的夹角∠A=30°,过C点的切线与AB的延长线交于点P. 如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.