题目内容
6.P是正方形ABCD的BC边上一点,连结AP,AB=8,BP=3,Q是线段AP上一动点,连结BQ并延长交四边形ABCD的一边于点R,若点Q是BR的三等分点,则AR的长为$\frac{3}{2}$或6或$\frac{8\sqrt{13}}{3}$.分析 分三种情形:①如图1中,当BQ1=2Q1R1时,②如图1中,当Q2R2=2BQ2时,③如图2中,当点R3在CD上时,R3Q3=2BQ3,作R3M⊥AB于M,交AP于N.分别利用平行线的性质,勾股定理等知识即可解决.
解答 解:如图1中,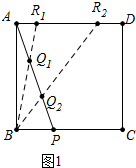 ①当BQ1=2Q1R1时,
①当BQ1=2Q1R1时,
∵AD∥BC,
∴$\frac{A{R}_{1}}{PB}$=$\frac{{Q}_{1}{R}_{1}}{B{Q}_{1}}$=$\frac{1}{2}$,∵PB=3,
∴AR1=$\frac{3}{2}$,
②当Q2R2=2BQ2时,
∵AR2∥PB,
∴$\frac{A{R}_{2}}{PB}$=$\frac{{Q}_{2}{R}_{2}}{B{Q}_{2}}$=2,
∴AR2=6.
③如图2中,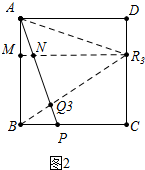 当点R3在CD上时,R3Q3=2BQ3,作R3M⊥AB于M,交AP于N.
当点R3在CD上时,R3Q3=2BQ3,作R3M⊥AB于M,交AP于N.
∵R3N∥PB,
∴$\frac{{R}_{3}N}{PB}$=$\frac{{R}_{3}{Q}_{3}}{B{Q}_{3}}$=2,
∴NR3=6,MN=MR3=AD=8-6=2,
∵MN∥PB,
∴$\frac{MN}{PB}$=$\frac{AM}{AB}$,
∴AM=$\frac{16}{3}$,
在RT△AMR3中,AR3=$\sqrt{A{M}^{2}+M{{R}_{3}}^{2}}$=$\sqrt{(\frac{16}{3})^{2}+{8}^{2}}$=$\frac{8\sqrt{13}}{3}$.
故答案为$\frac{3}{2}$或6或$\frac{8\sqrt{13}}{3}$.
点评 本题考查正方形的性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是正确画出图形,学会分类讨论的思想,属于中考常考题型.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
17. 如图所示,几何体的左视图是( )
如图所示,几何体的左视图是( )
 如图所示,几何体的左视图是( )
如图所示,几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
18.下列命题不正确的是( )
| A. | 0是整式 | B. | x=0是一元一次方程 | ||
| C. | (x+1)(x-1)=x2+x是一元二次方程 | D. | $\sqrt{4}$是二次根式 |
 如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )
如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )



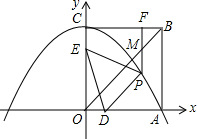 如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含点A,C),过P点作PF⊥BC于点F,点D,E的坐标分别为D(1,0),E(0,3).连接DE,PD,PE,OB.
如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含点A,C),过P点作PF⊥BC于点F,点D,E的坐标分别为D(1,0),E(0,3).连接DE,PD,PE,OB.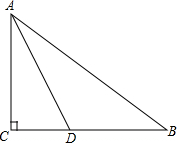 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.
如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.