题目内容
19.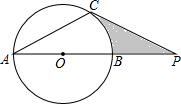 如图,⊙O直径AB与弦AC的夹角∠A=30°,过C点的切线与AB的延长线交于点P.
如图,⊙O直径AB与弦AC的夹角∠A=30°,过C点的切线与AB的延长线交于点P.(1)求证:CA=CP;
(2)已知⊙O的半径r=$\sqrt{6}$,求图中阴影部分的面积S.
分析 (1)求出∠ACO=∠A=30°,根据三角形外角性质求出∠COB=60°,求出∠P,即可得出答案;
(2)解直角三角形求出PC,求出△OCP和扇形COB的面积,即可得出答案.
解答 (1)证明:连接OC,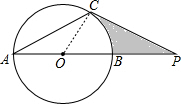
∵OA=OC,∠A=30°,
∴∠ACO=∠A=30°,
∴∠COB=∠A+∠ACO=60°,
∵PC为⊙O的切线,
∴∠OCP=90°,
∴∠P=30°,
∴∠A=∠P,
∴AC=PC;
(2)解:在Rt△OCP中,CP=OC×tan60°=$\sqrt{6}$×$\sqrt{3}$=3$\sqrt{2}$,
所以图中阴影部分的面积是:
S=S△OCP-S扇形COB
=$\frac{1}{2}×3\sqrt{2}×\sqrt{6}$-$\frac{60π×(\sqrt{6})^{2}}{360}$
=3$\sqrt{3}$-π.
点评 本题考查了等腰三角形的性质和判定,切线的性质,解直角三角形,扇形的面积的应用,能熟记知识点是解此题的关键.

练习册系列答案
相关题目
7.某市轨道交通3号线全长32.83千米,32.83千米用科学记数法表示为( )
| A. | 3.283×104米 | B. | 32.83×104米 | C. | 3.283×105米 | D. | 3.283×103米 |
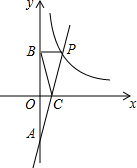 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(2,4),与y轴交于点A(0,-4),与x轴交于点C,PB⊥y轴于点B.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(2,4),与y轴交于点A(0,-4),与x轴交于点C,PB⊥y轴于点B. 由几个小正方体搭成的几何体,其主视图、左视图相同,均如图所示,则搭成这个几何体最少需要3个小正方体.
由几个小正方体搭成的几何体,其主视图、左视图相同,均如图所示,则搭成这个几何体最少需要3个小正方体. 如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )
如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )



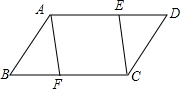 已知:如图,E、F分别是平行四边形ABCD边AD、BC上的点,并且AF∥CE,
已知:如图,E、F分别是平行四边形ABCD边AD、BC上的点,并且AF∥CE, 如图,将三角板的直角顶点放在直尺的一边上,若∠1=68°,则∠2的度数为22°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=68°,则∠2的度数为22°.