题目内容
6.已知关于x的一元二次方程x2-2x+k-1=0.(1)若此方程有两个不相等的实数根,求实数k的取值范围;
(2)已知x=3是此方程的一个根,求方程的另一个根及k的值;
(3)当Rt△ABC的斜边长c=$\sqrt{3}$,且两条直角边a和b恰好是这个方程的两个根时,求Rt△ABC的面积.
分析 (1)根据一元二次方程x2-2x+k-1=0有两个不相等的实数根,列出k的不等式,求出k的取值范围;
(2)把x=3代入方程,求出k的值,进而解方程,求出另一个根;
(3)根据题意可得a2+b2=($\sqrt{3}$)2,再根据根与系数关系得到a+b=2,ab=k-1,进而得到k的方程,求出k的值,即可求出Rt△ABC的面积.
解答 解:(1)∵关于x的一元二次方程x2-2x+k-1=0,方程有两个不相等的实数根,
∴△>0,即△=4-4(k-1)>0,
∴k<2;
(2)∵x=3是此方程的一个根,
∴把x=3代入原方程得:9-6+k-1=0,解得k=-2,
∴原方程为x2-2x-3=0,
解得:x1=-1,x2=3,
∴方程另一个根是-1,k=-2;
(3)∵Rt△ABC的斜边长c=$\sqrt{3}$,且两条直角边a和b恰好是这个方程的两个根,
∴a+b=2,ab=k-1,
∵a2+b2=($\sqrt{3}$)2,
∴(a+b)2-2ab=a2+b2=3,
∴22-2(k-1)=3,解得k=$\frac{3}{2}$,
∴ab=k-1=$\frac{1}{2}$,
∴S△ABC=$\frac{1}{2}$ab=$\frac{1}{4}$.
点评 本题主要考查了根的判别式、因式分解法解一元二次方程、根与系数的关系以及勾股定理的知识,解答本题的关键是求出k的取值范围,此题难度一般.

练习册系列答案
相关题目
16.-3的倒数为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
1.一个不透明的布袋中有分别标着数字1、2、3、6的四个乒乓球(除标数不同外,没有其它区别),现从袋中随机一次摸出两个乒乓球,则这两个球上的数字之积为6的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
18.某市交通部门为了有力制止酒驾行为拟制了一份“克服酒驾几种方式”的调查问卷,并在该市司机中进行了抽样调查.调查问卷如表:
现整理调查问卷并制作了统计图:
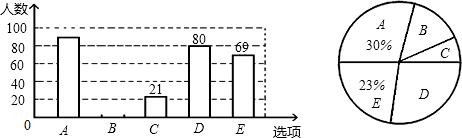
根据上述信息,解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若该市有30000名司机,估计支持D选项的司机大约有多少人?
| 克服酒驾--你认为哪种方式最好?(单选) |
| A、加强宣传,增强意识. B、在汽车上张贴“请勿酒驾”字样. C、司机上岗前签“拒接酒驾”保证书. D、加大检查力度,严惩酒驾行为. E、查出酒驾追究整个家庭责任. |

根据上述信息,解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若该市有30000名司机,估计支持D选项的司机大约有多少人?
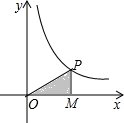 如图,点P为反比例函数y=$\frac{16}{x}$在第一象限图象上的动点,过点P作x轴的垂线,垂足为M,则三角形OPM的面积为8.
如图,点P为反比例函数y=$\frac{16}{x}$在第一象限图象上的动点,过点P作x轴的垂线,垂足为M,则三角形OPM的面积为8.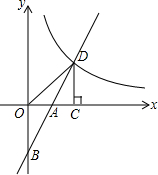 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD.
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD.