题目内容
11.对于实数x,我们规定[x]表示不大于x的最大整数,如[4]=4,[$\sqrt{3}$]=1,[-2.5]=-3,现对82进行如下操作:82$\stackrel{第1次}{→}$[$\frac{82}{\sqrt{82}}$]=9$\stackrel{第2次}{→}$[$\frac{9}{3}$]=3$\stackrel{第3次}{→}$[$\frac{3}{\sqrt{3}}$]=1,这样对82只需进行3次操作后变为1,类似地,按照以上操作,只需进行3次操作后变为1的所有正整数中,最大的正整数是255.分析 根据[x]表示不大于x的最大整数,可得答案.
解答 解:255→$[\frac{255}{\sqrt{255}}]=15$→$[\frac{15}{\sqrt{15}}]=3$→$[\frac{3}{\sqrt{3}}]=1$,
故答案为:255.
点评 本题考查了估算无理数的大小,解决本题的关键是明确[x]表示不大于x的最大整数.

练习册系列答案
相关题目
2.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
1.下列几何体中,俯视图相同的是( )


| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
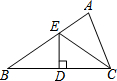 如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
 如图由7个大小相同的正方体摆成的立体图形,它的俯视图是( )
如图由7个大小相同的正方体摆成的立体图形,它的俯视图是( )



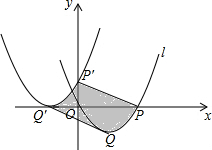 如图,抛物线l:y=2x2-2x,将该抛物线向左并向上平移,使顶点Q的对应点是Q′,抛物线l与x轴的右交点P的对应点是P′,点P′、Q′都在坐标轴上,则在这个平移的过程中,抛物线l上曲线段PQ扫过的面积(即图中阴影部分的面积)为$\frac{3}{4}$.
如图,抛物线l:y=2x2-2x,将该抛物线向左并向上平移,使顶点Q的对应点是Q′,抛物线l与x轴的右交点P的对应点是P′,点P′、Q′都在坐标轴上,则在这个平移的过程中,抛物线l上曲线段PQ扫过的面积(即图中阴影部分的面积)为$\frac{3}{4}$.